
Full resolution (TIFF) - On this page / på denna sida - Landkort

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Udfoldningsprojektioner har dog saa ringe
Tilknytning til Hjælpefladen, at de egl. lige saa godt
kunde henregnes til Azimutalprojektion,
ligesom ogsaa det omvendte er Tilfældet.
Ved perspektivisk Projektion med Øjepunkt
i Jordcentret kan Gradnettet overføres paa en
Kegle, som tangerer Kuglen langs en Parallel.
Meridianerne bliver da rette Linier, der skærer
hverandre i Keglens Toppunkt, og Parallellerne
koncentriske Cirkler om dette Punkt.
Tangeringsparallellen bliver længdetro, men i øvrigt
vokser Forvanskningen stærkt til begge Sider
af denne Parallel. Ved at benytte en skærende
Kegle faas to længdetro Paralleller, og for større
Dele af Jorden kan anvendes fl. Kegler, saa at
hvert Bælte af passende Bredde overføres paa
sin Kegle. En saadan Projektion kaldes
polykonisk. Meridianer, og Paralleller kan ogsaa
overføres ved deres Planers Skæring med
Keglefladen (Fig. 8); men det ses let, at alle
Parallellerne aa, bb, ... med Undtagelse af den
tangerende cc bliver for store. Det samme
gælder Meridianstykkerne mod Ækvator, medens
disse mod Polen bliver for smaa. Herpaa kan
der hjælpes noget ved at anvende en skærende
Kegle (alm. kaldt de l’Isles Projektion), men
langt bedre Resultater kan dog, saavel med
tangerende som med skærende Kegle, opnaas
ved paa andre Maader at bestemme Længden
af de afskaarne Meridianstykker paa Keglen.
Konstrueres nemlig Parallellerne saaledes, at
disse Meridianstykker overalt faar samme
Længde som paa Kuglen, faar man en
længdetro konisk Projektion, og da dennes
Forvanskninger i andre Henseender er moderate,
benyttes den en Del. Parallellernes Radier kan
ogsaa beregnes dels saaledes, at Projektionen
bliver arealtro, og dels saaledes, at
Maalestoksforholdet i ethvert Punkt bliver det
samme langs Parallellen som langs Meridianen. I
sidste Tilfælde faas den konforme
Kegleprojektion, som nu er anvendt ved alle
den danske Generalstabs Kort. Keglen tangerer
her langs Parallellen 56°, hvor Kortbilledet
altsaa bliver helt rigtigt, men Afstandene
forstørres, efterhaanden som man fjerner sig fra
denne Parallel, dog er Maksimum (ved Skagen)
kun c. 0,03 %.
Ved alle de foran betragtede koniske
Projektioner fremstilles Meridianerne som rette
Linier, hvis indbyrdes Vinkel bliver θsinφ0,
hvor θ er den geografiske Længdeforskel
mellem de paagældende Meridianer, og φ0
Tangeringsparallellens Bredde. Anderledes
derimod ved den mere vilkaarlige Bonne’s
Projektion, der er arealtro og konstrueres
saaledes: Ved Udfoldning af Keglefladen
fremkommer Tangeringsparallellen, og koncentrisk med
denne trækkes Cirkler med samme indbyrdes
Afstand som de Paralleller, de fremstiller.
Midtemeridianen er en ret Linie, de øvrige
Meridianer bliver derimod krumme Linier, idet
de bestemmes saaledes, at de mellemfaldende
Stykker af
Parallellerne faar deres
rigtige Længde.
Projektionen (Fig.
9) er altsaa
ogsaa længdetro
langs Parallellerne
og
Midtemeridianen, men anvendt
paa større Dele
af Jorden giver
den en betydelig
Vinkelforvanskning. Den har været meget anvendt, tidligere
bl. a. ved de danske Generalstabskort under
det misvisende Navn, »modificerede
Flamsted’ske« Projektion.
III. Cylinderprojektioner. Som alt
bemærket er disse spc. Tilfælde af
Kegleprojektionerne. Til Bonne’s Projektion svarer saaledes
Sanson’s (ogsaa kaldt Flamsted’s Projektion),
hvor Ækvator, langs hvilken Cylinderen
tangerer, tilligemed alle Paralleller bliver rette
Linier vinkelrette paa Midtemeridianen. De
saakaldte plat-kvadratiske og
platrektangulære Kort, der i 15. og 16. Aarh.
anvendtes som Søkort, konstrueredes efter et
i øvrigt fra Oldtiden stammende Princip, hvor
man overførte Meridianerne ved deres Planers
Skæring med en Cylinder, som ved de første
tangerede langs Ækvator og ved de sidste skar
Jorden langs en Parallel. Parallellerne
fremstilledes ogsaa som parallelle rette Linier med
samme indbyrdes Afstand som paa
Jordoverfladen. Hele Gradnettet bestod af lutter lige
store henh. Kvadrater og Rektangler. Den
samme Projektion, men i transversal Form, altsaa
med Cylinderen tangerende langs en Meridian,
benævnes nu efter Cassini, som i sidste
Halvdel af 18. Aarh. anvendte den til sit
berømte Kort over Frankrig. Cylinderprojektioner
kan selvfølgelig ogsaa konstrueres arealtro,
hvilket dog som Regel kun finder Sted for
Landene omkr. Ækvator. Langt større Bet. har
den konforme Cylinderprojektion, hvis
normale Form skyldes Mercator, som udtænkte
den, for at Loxodromen (s. d.) kunde blive en
ret Linie, der skar alle Meridianerne under
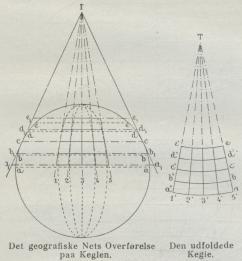 |
| Fig. 8 Det geografiske Nets Overførelse paa Keglen. Den udfoldede Kegle. |
 |
| Fig. 9. Bonne’s Projektion. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>