
Full resolution (TIFF) - On this page / på denna sida - Mikroskop

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Teorien for M.’s Billeddannelse.
Opløsningsevnen. Objektivet er M.’s
vigtigste Del; dets Fuldkommenhed bestemmer
Billedernes Godhed. Hvor fine og nøjagtigt
gengivne Enkelthederne i Billedet bliver,
bestemmes først og fremmest af, i hvor høj Grad
Objektivet formaar at faa Straaler, udgaaede
fra et bestemt Punkt, til atter at mødes i et
enkelt Punkt, altsaa af, hvor godt Linsefejlene
er ophævede. Men dertil kommer, at
Objektivets Evne til at adskille fine Detailler i
Objektet har en Grænse, der bestemmes af dets
numeriske Apertur, medens Brændvidden kun
bestemmer dets Forstørring. For at forstaa
dette og erfare, hvor langt man kan naa i
Fuldkommengørelsen af M., er den geometriskoptiske
Linseteori ikke tilstrækkelig, men man
maa gaa ind paa Lysets Bølgeteori. Den
fuldstændige Teori skyldes Abbe. Da den geom.
Optiks Lysstraaler ikke virkelig eksisterer, faar
den geom. Teoris Resultater først Gyldighed og
Betydning, naar deres Rigtighed ogsaa er
bevist ud fra Lysets Bølgeteori. Det, der virkelig
finder Sted ved en Billeddannelse i en Linse,
er, at de kugleformede Bølger, der udgaar fra
et Lyspunkt og træffer Linsen, derved omdannes
til konkave kugleformede Bølger med
Billedpunktet til Centrum. Hvorledes Lysfordelingen
i og omkr. Billedpunktet bliver, kan da
kun findes ved at undersøge Inteferensen af
Lyset fra de forsk. Dele af hver Bølge;
Resultatet af denne Interferens er Billedet af
Lyspunktet. Man finder, at selv i de Tilfælde, hvor
man efter den geom. Straalegang virkelig
skulde vente et punktformet Billede af det
betragtede Lyspunkt, faas kun en større ell. mindre
Tilnærmelse dertil, en Lysplet, omgivet af nogle
faa afvekslende mørke og lyse Ringe. Saaledes
bliver f. Eks. Billedet af en Stjerne i en astron.
Kikkert. Lyspletten nærmer sig desto mere til
et Punkt, og Ringene bliver desto svagere,
altsaa Billedet desto skarpere, jo større Lyskeglens
Toppunktsvinkel (»Aabning«) er. I Reglen
faas ved den geom. Optiks Regler en
overordentlig god Tilnærmelse til Virkeligheden.
Men herved er forudsat, at Objektet er
selvlysende, da kun i dette Tilfælde Lysstraalerne
fra et bestemt Punkt af det kan interferere
(er »kohærente«). Er Objektet belyst, saaledes
som det næsten altid er Tilfældet ved Brug af
M., tilbagekastes ell. spredes fra et bestemt af
dets Punkter Straaler, der stammer fra mange
forsk. Punkter af Lyskilden, og de kan ikke
interferere. Man skulde da vente, at der kun
kunde dannes Billede af Lyskilden, ikke af
Objektet. For at finde, om der ogsaa dannes
Billede af Objektet, maa man forfølge
Straalerne videre fra Lyskildens Billede og
undersøge, hvorledes de, der kan interferere, gør
det videre. Man finder da ganske vist, at i
Reglen faas ogsaa af ikke selvlysende Genstande
Billeder, der er meget gode Tilnærmelser til,
hvad den geom. Optik fører til, men netop
ved Brugen af M. støder man, fordi Objekterne
er saa smaa, ikke sjældent paa Tilfælde, hvor
den geom. Behandlings Ufuldkommenhed viser
sig grelt. Som Eksempel betragter vi Afbildningen
af et Gitter af afvekslende gennemsigtige
og uigennemsigtige ækvidistante Dele,
f. Eks. ækvidistante Linier, ridsede i en
forsølvet Glasplade. I Fig. 10 er G Gittret og CD
Objektivet. G tænkes belyst med parallelt
monokromattisk Lys af Bølgebredden λ. Foruden
det direkte Lys, der træffer Objektivet ved
C, vil der fra Gitteret udgaa afbøjet Lys,
Spektrene af 1., 2 . . . Orden til begge
Sider (se Bøjning); i Fig. er kun vist Spektrene til
den ene Side FD, FE. . . Det direkte Lys samles i
Objektivets Brændplan til et Billede A af den fjerne
Lyskilde og gaar videre op mod Okularet; de af de
afbøjede Lysbundter, der træffer Objektivet, danner
en Række andre Billeder af Lyskilden, Spektrene
af 1., 2. . . . Orden; i Fig. opfanges kun Bundterne af
1. Orden og danner Billedet B og et tilsvarende
paa den anden Side af A. Dette er den primære
Billeddannelse. Det, der interesserer her,
nemlig Billedet af Objektet G, faas ved at
undersøge, hvordan Straalerne CA, DB o. s. v.
interfererer højere oppe i Objektivets Billedplan.
Man finder, at dette sidste Billede, som
betragtes gennem Okularet, virkelig kommer til
at bestaa af ækvidistante lyse og mørke Linier
i den rigtige indbyrdes Afstand, altsaa bliver
et Billede af Gitteret, men kun i det Tilfælde,
at Objektivet foruden det direkte Lys opfanger
i det mindste et af Spektrene, og Ligheden
mellem Billede og Objekt bliver desto bedre,
jo flere Spektre, Objektivet opfanger. Hvis
Objektivet er saa lille, at kun det direkte Lys FC
opfanges, faas ingen afvekslende lyse og
mørke Striber, men kun en ensformig lysende
Flade af den rigtige Størrelse; i dette Tilfælde
vil M.’s Billede af Gitteret altsaa være
fuldstændig falsk, ikke vise Spor af Gitterets
»Struktur«.
Man kan nu finde Betingelsen for, at M.
netop formaar at adskille (»opløse«) Gitterets
Striber. Fra Bøjningsteorien har man, at
Afbøjningen v for Spektret af 1. Orden er bestemt
ved sin v = λ/e, hvor e er Afstanden mellem
Gitterstregerne. For at første Spektrum skal
opfanges maa v < u, altsaa skal sin u > λ/e.
Det samme gælder for Adskillelsen af tæt
sammenliggende Punkter. Her er dog forudsat, at
Objektet befinder sig i Luft; er det lejret i et
Stof med Brydningsforhold n, der tillige
udfylder Rummet op til Objektivet, skal i St f.
sin u sættes n sin u, da λ bliver n Gange
mindre; n sin u er jo netop Objektivets numeriske
Apertur a. Den mindste Afstand e, hvori
Objektivet endnu kan adskille Punkter ell. Linier,
er altsaa e = λ/a. Regnes med Bølgebredden for
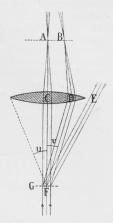 |
| Fig. 10. Afbildning af Gitter. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>