
Full resolution (TIFF) - On this page / på denna sida - Polarisation, Lysets

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Polirisatoren gaar en Straale videre, der kun
indeholder Svingninger i en bestemt Retning,
hvilket man udtrykker ved at sige, at den er
lineært ell. plant polariseret
(plansat). Den polariserede Straales
Svingningsretning er alene bestemt ved Polarisatorens
Orientering. Fig. 3 skal anskueliggøre, hvordan
det i Fig. 1 viste
Straalebundt kommer
til at se ud efter at
være blevet linieært
polariseret ved at
have passeret en
Polarisator med lodret
Svingningsretning.
Det er klart, at en
saadan Straale maa
forholde sig forsk. i
forsk. Retninger
vinkelret paa Straalen,
f. Eks. i de 2 ved Pilene a og b antydede
Retninger.
Til Paavisning af denne Forskel bruges en
Analysator. Som Analysator kan enhver
Polarisator tjene. Sendes nemlig det allerede
lineært polariserede Lys ind mod en anden
Polarisator, som vi i det flg. vil kalde
Analysatoren, vil Lysets retlinede Svingninger igen
blive opløst i 2 paa hinanden vinkelrette
Komposanter, hvoraf kun den ene slipper igennem.
Dette betyder, at Lyset i Alm. svækkes ved at
passere Analysatoren, da hver Komposant er
mindre end den opr. Svingning, og Lysets
Intensitet er proportional med Kvadratet paa det
største Udsving (Amplituden). Svækkelsen er
desto mindre, jo mindre Vinklen mellem
Lysets og Analysatorens Svingningsretning er, og
Lyset passerer helt usvækket, naar dets
Svingningsretning falder sammen med Analysatorens,
medens omvendt slet intet Lys slipper igennem
Analysatoren, naar dets Svingningsretning staar
vinkelret paa Analysatorens, da der i dette
Tilfælde slet intet bliver tilovers til den
Komposant, der kan slippe gennem Analysatoren. Om
en Straale er plant polariseret ell. naturlig
(ikke polariseret), undersøges altsaa ved at
sende den gennem en som Analysator tjenende
Polarisator, som drejes saaledes, at dens
Svingningsretning beskriver en Plan vinkelret paa
Straalen. Er Straalen polariseret, skal Styrken
af det Lys. der slipper gennem Analysatoren,
variere regelmæssigt under Drejningen
(nemlig være proportional med cos2v, hvor v er
Vinklen mellem det polariserede Lys’ og
Analysatorens Svingningsretning); specielt skal Lyset
fuldstændig udslukkes for 2 Stillinger af
Analysatoren, 180° fra hinanden, og være
fuldstændig usvækket for de 2 Stillinger midt imellem.
En naturlig ikke polariseret Lysstraale derimod
ændrer ikke sin Styrke under Drejningen, men
svækkes for alle Stillinger af Analysatoren til
Halvdelen af sin opr. Styrke. Her er dog visse
Undtagelser, som omtales ndf. Endelig vil en
delvis polariseret Straale, der kan opfattes som
en Blanding af naturligt og polariseret Lys,
kunne kendes, ved at den vel ændrer sin
Styrke under Drejningen, men ikke fuldstændig
udslukkes for nogen Stilling af Analysatoren.
P. ved Tilbagekastning er det
simpleste Tilfælde af P. (Malus, 1808). For
ethvert gennemsigtigt isotropt (ikke krystallinsk)
Stof eksisterer der en bestemt Indfaldsvinkel.
Polarisationsvinklen, for hvilken den
tilbagekastede Straale er fuldstændig
polariseret; for alle andre Indfaldsvinkler er den
tilbagekastede Straale delvis polariseret og desto
mere, jo nærmere Indfaldsvinklen ligger ved
Polarisationsvinklen. Denne er bestemt, ved at
den tilbagekastede og den brudte Straale skal
staa vinkelret paa hinanden, hvilket giver, at
Tangens til Polarisationsvinklen skal være lig
Stoffets Brydningsforhold (Brewster’s Lov).
For alm. Glas med Brydningsforholdet 1,52
bliver Polarisationsvinklen c. 57°, for Vand c. 53°.
I Fig. 4 forestiller P1 et Stykke plant
Spejlglas, der rammes af en Lysstraale SA under
en Indfaldsvinkel SAI = 57°
(Polarisationsvinklen). Straalen er upolariseret, hvilket
symbolsk er antydet ved Streger og Prikker hen ad
Straalen, idet man, som vi saa, kan opløse
Svingningerne i Straalen i 2 paa hinanden
vinkelrette Komposanter, som vi her har valgt
liggende i Indfaldsplanen SAI (Stregerne) og
vinkelret derpaa (Prikkerne). Den Del AF af
Straalen, der kastes tilbage, er da fuldstændig
polariseret med Svingninger vinkelret paa
Indfaldsplanen, saa at dens Svingningstilstand skal
fremstilles ved lutter Prikker. For at paavise
dette kan man simplest bruge en anden
Glasplade P2, Mage til den første, som Analysator.
Den skal efter det tidligere omtalte kunne drejes
om den indfaldende Straale AF som Akse,
hvilket kan opnaas ved at befæste den til en Stang
HK i Forlængelsen af AF og dreje den om
denne. Under Drejningen vil AF stadig ramme P2
under en Indfaldsvinkel lig
Polarisationsvinklen, saa at den tilbagekastede Straale FG
beskriver en Kegleflade om AF; men AF’s
Svingninger vil forandre deres Beliggenhed i Forhold
til Indfaldsplanen, og derfor vil FG forandre
sin Styrke under denne Drejning. I den
tegnede Stilling er Tilbagekastningen ret rigelig
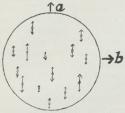 |
| Fig. 3. Polariseret Lys. |
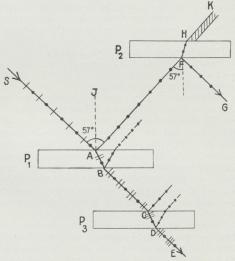 |
| Fig. 4. Polarisation ved Tilbagekastning. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>