
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
96
TEKNISK TIDSKRIFT
21 dec. 1929
eller ^ =
Qt V^ HS Q2V2*H2* P2 Q2V2*H2*
eller slutligen, om värdet på Fi : V2 insättes,
Pi Qi 9i Hi3
P 2 02 02 H23-
iVi Pl gi3/2 tf I7/2
På samma sätt erhålles — = –„, ., .
iV2 g23l2 2
Om man här antager <7X — g2 och = (samma
medium med samma temperatur vid de två fenomenen)
kommer man tydligen till den av W. Froude
framställda lagen för restmotstånden av två likformiga
fartyg vid korresponderande hastigheter:
Pi
= = linjära skalan upphöjd till 3
resp.
H_
Ni = HJ[2
N2 HJI2
vid
Vi
V2
HSI*
H 0V2
7/2
kvadratroten ur den linjära skalan.
Vi ha givetvis anledning att referera till
restmot-ståndet för fartyg i detta sammanhang, då ju
begreppet restmotstånd inrymmer liknande antagande, som
här gjorts, i det man antager att detsamma utgör den
del av det totala motståndet, som beror av
tyngdkraftens verkan (vågbildningen).
Man kan säga att man här kommit till en
generalisering av Froude’s modellregel för restmotståndet,
då vi ju kommit till uttryck, som ge oss möjlighet att
använda ett annat medium (med annat q) för
modellen än för fartyget, ävenså att korrigera för
variationen av g på olika orter.
Vi skola härefter antaga att endast krafter, som
bero av mediets viskositet, förefinnas. Motståndet
förutsattes således oberoende av tyngdkraftens
inverkan. dvs. exponenten d i ekv. (a) är — 0. Man
ser lätt att ekvationerna (b) då få formen
N
(VII
g V2 H2
pFStfi-^U
(d)
Dessa ekvationer representera Reynolds’ modellregel,
som säger att om vid två geometriskt likformiga
fenomen de Reynoldska talen äro lika:
11 H\ V2 H2
Vi
v2
så gäller att
Pi
Po
Qi Fi Hi Q2 IV U*
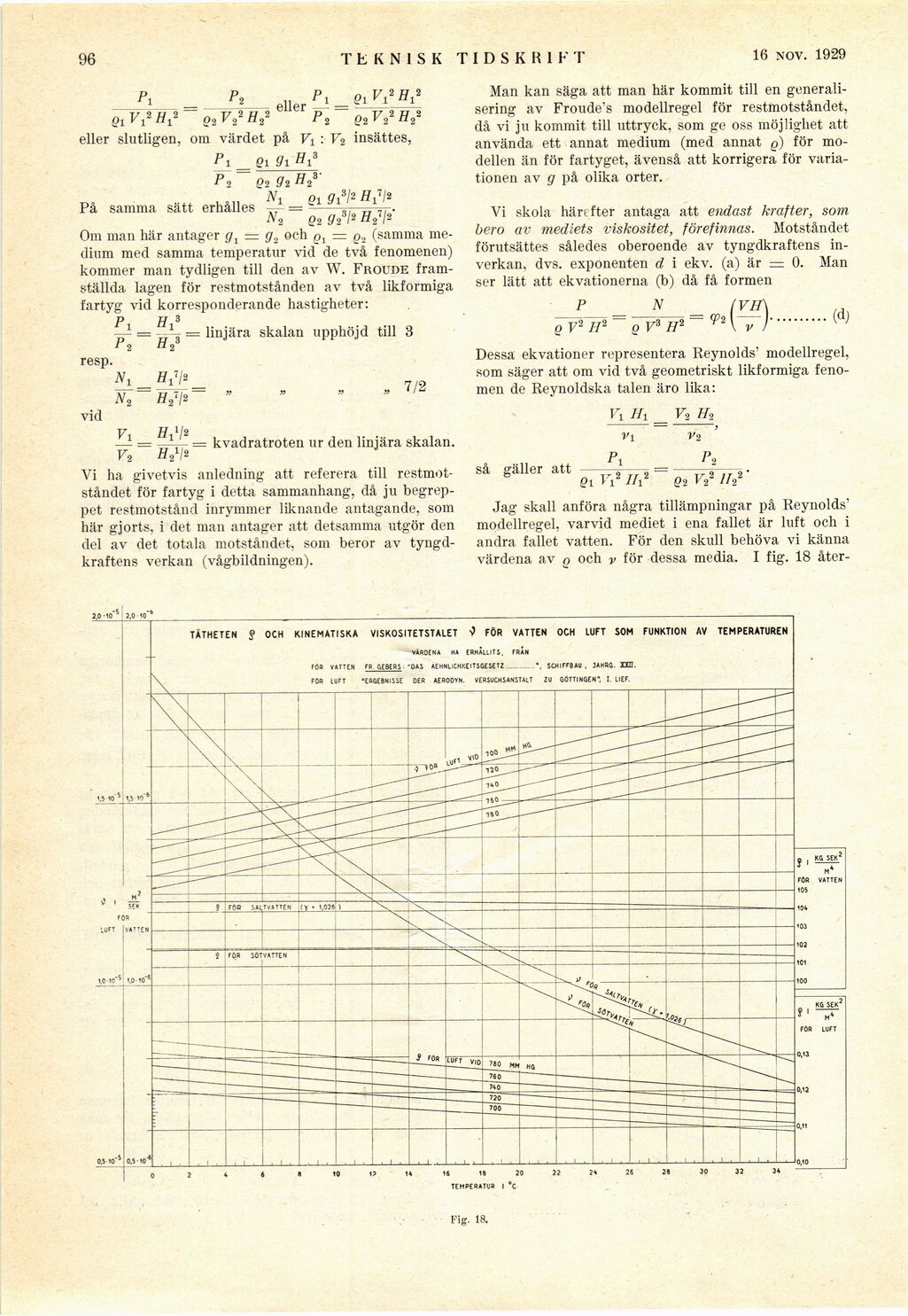
Jag skall anföra några tillämpningar på Reynolds’
modellregel, varvid mediet i ena fallet är luft och i
andra fallet vatten. För den skull behöva vi känna
värdena av o och v för dessa media. I fig. 18 åter-
Fig. 5. Fig. 7.
<< prev. page << föreg. sida << >> nästa sida >> next page >>