
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
100
TEKNISK TIDSKRIFT
20 SePt. 1930
Därmed bestämmas radierna hos cirklarna genom
följande relationer
^ kg
R + r
7 ~ G~ fi>
Då erhålles
och
Q3
k2
ß
■ß
■ R.
7Z
’rif
kg
r = ß._+
Q2
k2
R =
7 Gl
dt + i2
V /?2
y(y + ß) V ß2
Förhållandet mellan radierna blir
Inför man nu beteckningen
y
n = 4
(25)
(26)
(27)
(28)
så blir
Alltefter som r
R
— = n ■
>Gy ’ . A
<y*-ß2\}
+
Q2
ar epicy-
y — ß2 Vy2 ’ Å
kloiden förkortad, vanlig eller förlängd.
Genom införandet av den nyss gjorda
beteckningen för ,’ =n kan behandlingen av problemet
ß
ytterligare förenklas på följande sätt.
k G
ß). Relationen mellan n, — och
Gl bl
Återgår man till ekv. (17), så finner man att
förhållandet mellan y och ß kan angivas till
V + \/p2 — I2
n* =
eller
i -y’p2-
W2 + 1
n
(29)
(30)
varur, efter begagnandet av formlerna 12 och 13,
k
förhållandet — kan beräknas till
Gi
k
Gi
(31)
k
Denna formel anger sålunda värdet av — så snart
Gt
n av en eller annan anledning för ett visst fall är
bestämd.
k
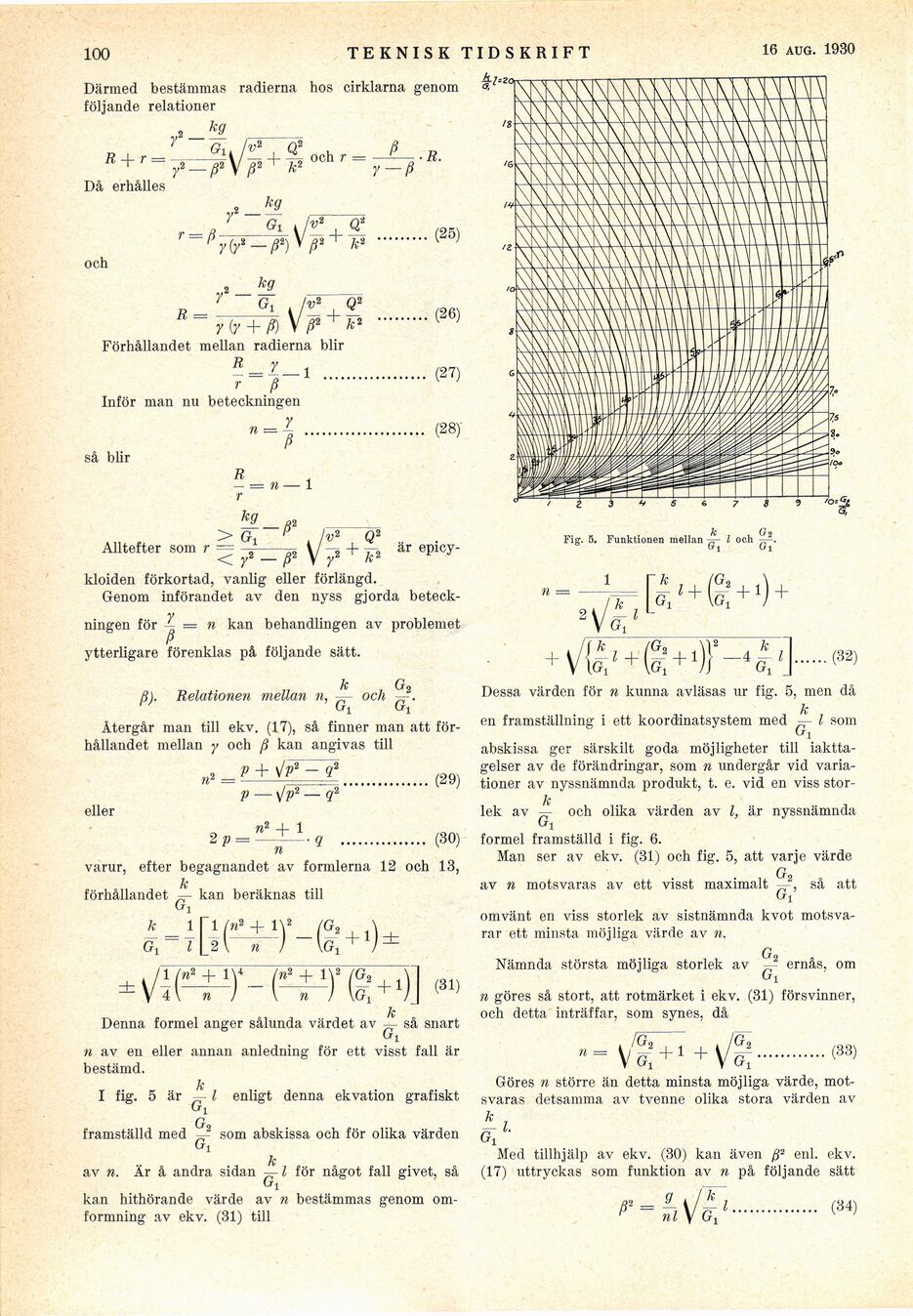
I fig. 5 är - I enligt denna ekvation grafiskt
"i
Q,
framställd med ~ som abskissa och för olika värden
Gi
k
av n. Är å andra sidan — l för något fall givet, så
Gi
kan hithörande värde av n bestämmas genom
omformning av ekv. (31) till
Fig. 5. Funktionen mellan ~ l och
fri Gl
n =
^R-SH
+
+
......
(32)
Dessa värden för n kunna avläsas ur fig. 5, men då
k
en framställning i ett koordinatsystem med — l som
Gi
abskissa ger särskilt goda möjligheter till
iakttagelser av de förändringar, som n undergår vid
variationer av nyssnämnda produkt, t. e. vid en viss
stor-k
lek av — och olika värden av l, är nyssnämnda
Gi
formel framställd i fig. 6.
Man ser av ekv. (31) och fig. 5, att varje värde
av n motsvaras av ett visst maximalt
G2
så att
omvänt en viss storlek av sistnämnda kvot
motsvarar ett minsta möjliga värde av n.
G
Nämnda största möjliga storlek av r2 ernås, om
G i
n göres så stort, att rotmärket i ekv. (31) försvinner,
och detta inträffar, som synes, då
(33)
Göres n större än detta minsta möjliga värde,
motsvaras detsamma av tvenne olika stora värden av
k
G,
l.
Med tillhjälp av ekv. (30) kan även ß2 enl. ekv.
(17) uttryckas som funktion av n på följande sätt
ß2
9_
ni
V/*’-
(34)
<< prev. page << föreg. sida << >> nästa sida >> next page >>