Teknisk Tidskrift / 1933. Mekanik / 27 (1871-1962) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Häfte 3. Mars 1933 - Hjalmar O. Dahl: Största tillåtna sughöjden vid turbiner och centrifugalpumpar

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

approximativt beräkna den antagliga tryckminskningen.
Strömningen blir likvärdig med en rent transversell dylik
och tryck- och hastighetsförhållanden desamma som
i ett stillastående system med absoluta hastigheten w.

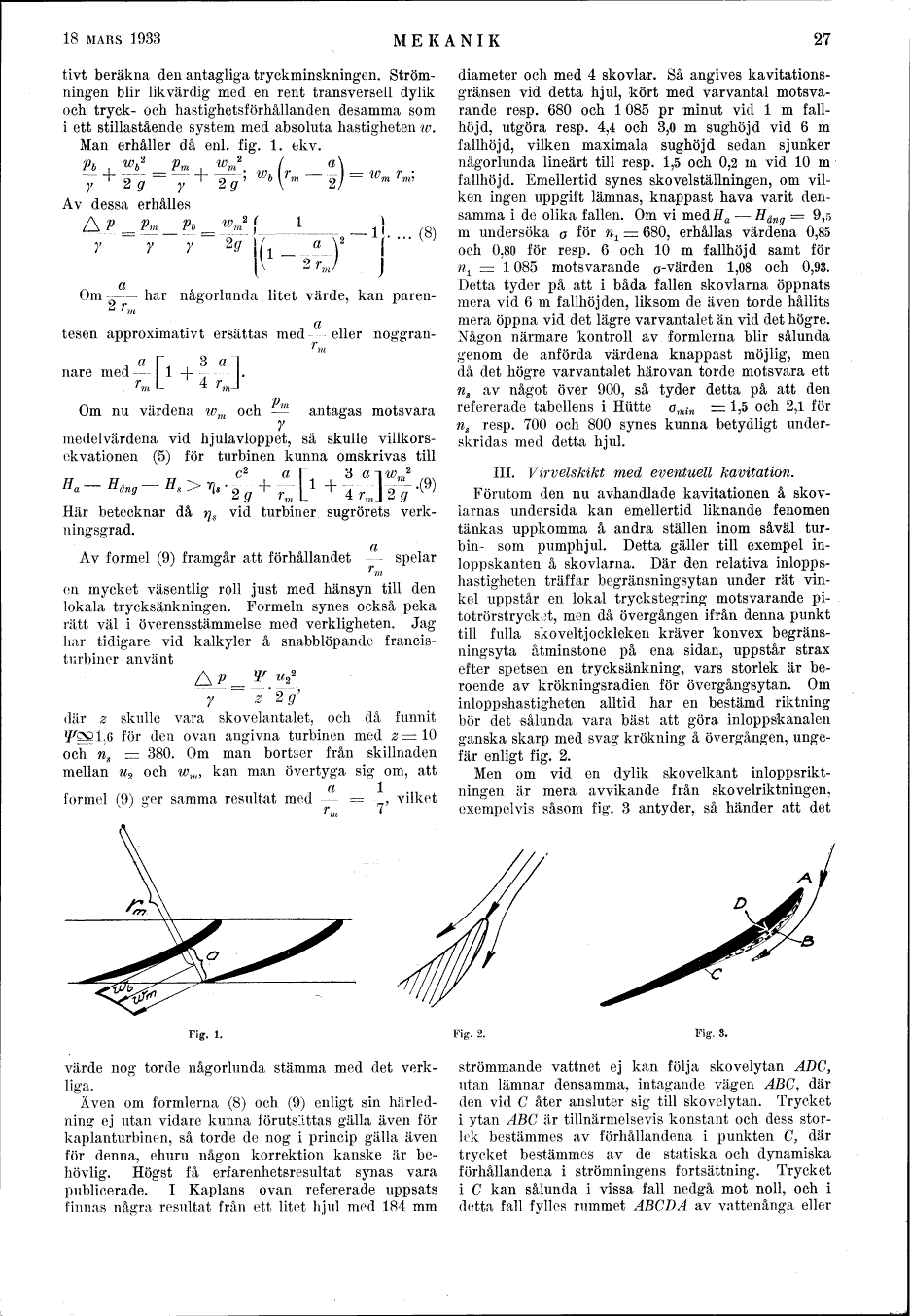
Man erhåller då enl. fig. 1. ekv.

pb		wb2		pm		wm2		a
–––	+	–––	=	–––	+	–––	; wb (rm –	–––	) = wm rm;
[gamma]		2 g		[gamma]		2 g		2

Av dessa erhålles

/_\ p		pm		pb		wm2		1
–––––	=	–––	–	–––	=	–––	{	––––––––	– 1 } . . . (8)
[gamma]		[gamma]		[gamma]		2g		(1 – a / 2 rm)2

	a
Om	–––	har någorlunda litet värde, kan parentesen
	2 rm

	a
approximativt ersättas med	–––	eller noggrannare med
	rm

a		3 a
–––	[ 1 +	–––––	].
rm		4 rm

	pm
Om nu värdena wm och ––––	antagas motsvara

medelvärdena vid hjulavloppet, så skulle
villkorsekvationen (5) för turbinen kunna omskrivas till

	c2		a		3 a		wm2
Ha – Hång – Hs > [eta]s	–––	+	–––	[ 1 +	–––––	]	–––	. . . . (9)
	2 g		rm		4 rm		2 g

Här betecknar då [eta]_s vid turbiner sugrörets
verkningsgrad.

	a
Av formel (9) framgår att förhållandet	–––	spelar
	rm

en mycket väsentlig roll just med hänsyn till den
lokala trycksänkningen. Formeln synes också peka
rätt väl i överensstämmelse med verkligheten. Jag
har tidigare vid kalkyler å snabblöpande
francisturbiner använt

/_\ p		[psi]		u22
–––––	=	–––	.	–––––	,
[gamma]		z		2 g

där z skulle vara skovelantalet, och då funnit
[psi]oo= 1,6 för den ovan angivna turbinen med z = 10
och n_s = 380. Om man bortser från skillnaden
mellan u₂ och w_m, kan man övertyga sig om, att

	a		1
formel (9) ger samma resultat med	–––	=	–––	. vilket
	rm		7

Fig. 1.	Fig. 2.	Fig. 3

värde nog torde någorlunda stämma med det verkliga.

Även om formlerna (8) och (9) enligt sin
härledning ej utan vidare kunna förutsättas gälla även för
kaplanturbinen, så torde de nog i princip gälla även
för denna, ehuru någon korrektion kanske är
behövlig. Högst få erfarenhetsresultat synas vara
publicerade. I Kap lans ovan refererade uppsats
finnas några resultat från ett litet hjul med 184 mm
diameter och med 4 skövlar. Så angives
kavitationsgränsen vid detta hjul, kört med varvantal
motsvarande resp. 680 och 1 085 pr minut vid 1 m
fallhöjd, utgöra resp. 4,4 och 3,0 m sughöjd vid 6 m
fallhöjd, vilken maximala sughöjd sedan sjunker
någorlunda lineärt till resp. 1,5 och 0,2 m vid 10 m
fallhöjd. Emellertid synes skovelställnmgen, om
vilken ingen uppgift lämnas, knappast hava varit
densamma i de olika fallen. Om vi med H_a – H_ång = 9,5
m undersöka o för n₁ = 680, erhållas värdena 0,85
och 0,80 för resp. 6 och 10 m fallhöjd samt för
n₁ = 1 085 motsvarande o-värden 1,08 och 0,93.
Detta tyder på att i båda fallen skovlarna öppnats
mera vid 6 m fallhöjden, liksom de även torde hållits
mera öppna vid det lägre varvantalet än vid det högre.
Någon närmare kontroll av formlerna blir sålunda
genom de anförda värdena knappast möjlig, men
då det högre varvantalet härovan torde motsvara ett
n_s av något över 900, så tyder detta på att den
refererade tabellens i Hütte o_min = 1,5 och 2,1 för
n_s resp. 700 och 800 synes kunna betydligt
underskridas med detta hjul.

III. Virvelskikt med eventuell kavitation.

Förutom den nu avhandlade kavitationen å
skovlarnas undersida kan emellertid liknande fenomen
tänkas uppkomma å andra ställen inom såväl
turbin- som pumphjul. Detta gäller till exempel
inloppskanten å skovlarna. Där den relativa
inloppshastigheten träffar begränsningsytan under rät
vinkel uppstår en lokal tryckstegring motsvarande
pitotrörstrycket, men då övergången ifrån denna punkt
till fulla skoveltjockleken kräver konvex
begränsningsyta åtminstone på ena sidan, uppstår strax
efter spetsen en trycksänkning, vars storlek är
beroende av krökningsradien för övergångsytan. Om
inloppshastigheten alltid har en bestämd riktning
bör det sålunda vara bäst att göra inloppskanalen
ganska skarp med svag krökning å övergången,
ungefär enligt fig. 2.

Men om vid en dylik skovelkant inloppsriktningen
är mera avvikande från skovelritningen,
exempelvis såsom fig. 3 antyder, så händer att det
strömmande vattnet ej kan följa skovelytan <i>ADC,<i>
utan lämnar densamma, intagande vägen ABC, där
den vid C åter ansluter sig till skovelytan. Trycket
i ytan ABC är tillnärmelsevis konstant och dess
storlek bestämmes av förhållandena i punkten C, där
trycket bestämmes av de statiska och dynamiska
förhållandena i strömningens fortsättning. Trycket
i C kan sålunda i vissa fall nedgå mot noll, och i
detta fall fylles rummet ABCDA av vattenånga eller

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>