Teknisk Tidskrift / 1934. Bergsvetenskap / 44 (1871-1962) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Häfte 6. Juni 1934 - Ernst Rothelius: Den moderna uppfattningen av krossningsarbetet

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

Den specifika ytenergien o, som åtgår för
uppdelning av en kristall efter en med kubsidan parallell
yta, var enligt Born

	1		U12
o =	––––	.	––––
	2		F

där U₁₂ är själva arbetet för att skilja kristalldelarna
åt och F den nybildade ytan på varje kristalldel. Den
totala nybildade ytan är då 2 F. Borns värden på

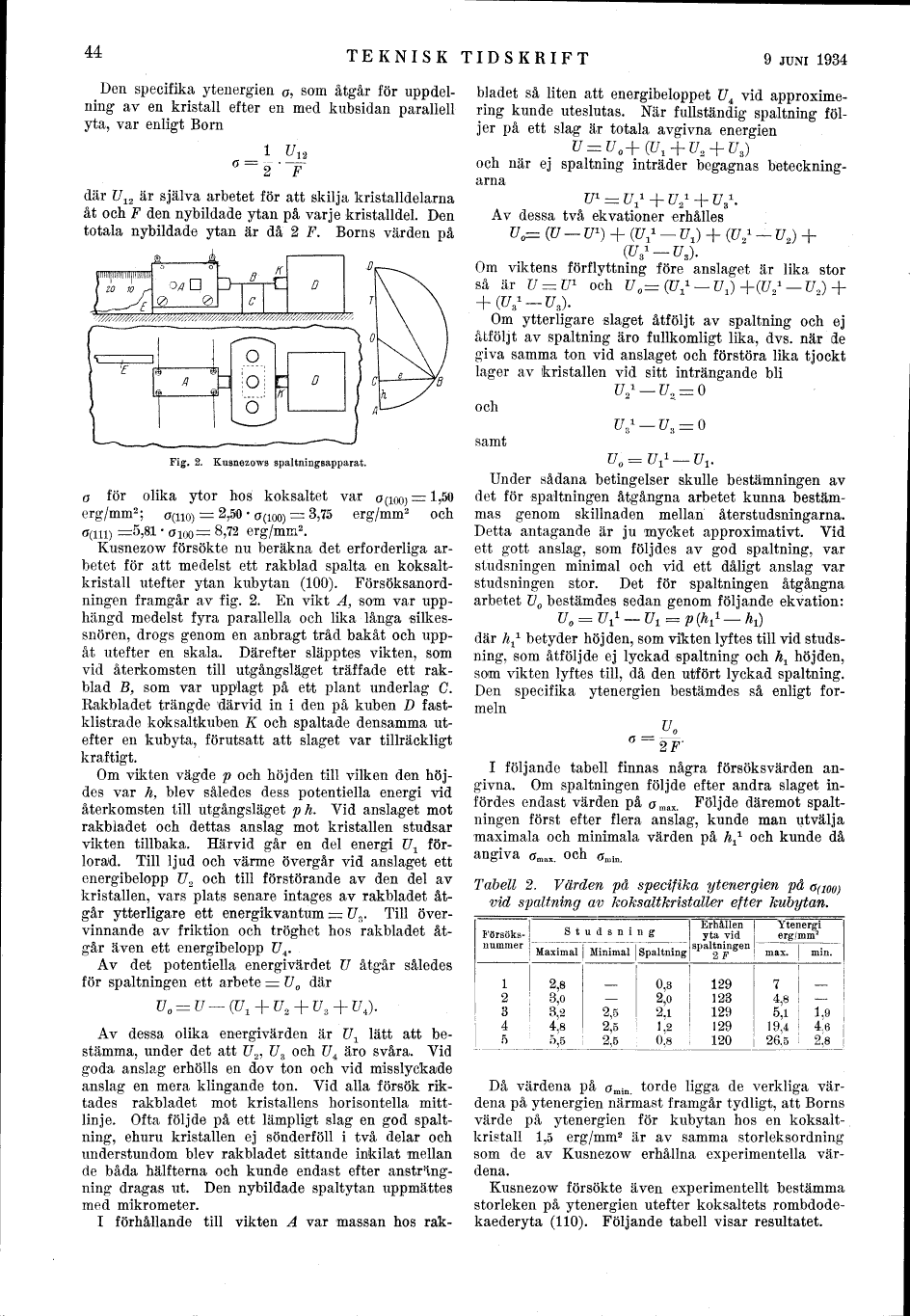
Fig. 2. Kusnezows spaltningsapparat.

o för olika ytor hos koksaltet var o₍₁₀₀₎ = 1,50
erg/mm²; o₍₁₁₀₎ = 2,50 ^. o₍₁₀₀₎ = 3,75 erg/mm² och
o₍₁₁₁₎ = 5,81 ^. o₁₀₀ = 8,72 erg/mm².

Kusnezow försökte nu beräkna det erforderliga
arbetet för att medelst ett rakblad spalta en
koksaltkristall utefter ytan kubytan (100).
Försöksanordningen framgår av fig. 2. En vikt A, som var
upphängd medelst fyra parallella och lika långa
silkessnören, drogs genom en anbragt tråd bakåt och
uppåt utefter en skala. Därefter släpptes vikten, som
vid återkomsten till utgångsläget träffade ett
rakblad B, som var upplagt på ett plant underlag C.
Rakbladet trängde därvid in i den på kuben D
fästklistrade koksaltkuben K och spaltade densamma
utefter en kubyta, förutsatt att slaget var tillräckligt kraftigt.

Om vikten vägde p och höjden till vilken den
höjdes var h, blev således dess potentiella energi vid
återkomsten till utgångsläget p h. Vid anslaget mot
rakbladet och dettas anslag mot kristallen studsar
vikten tillbaka. Härvid går en del energi U₁
förlorad. Till ljud och värme övergår vid anslaget ett
energibelopp U₂ och till förstörande av den del av
kristallen, vars plats senare intages av rakbladet
åtgår ytterligare ett energikvantum = U₃. Till
övervinnande av friktion och tröghet hos rakbladet
åtgår även ett energibelopp U₄.

Av det potentiella energivärdet U åtgår således
för spaltningen ett arbete = U₀ där
U₀ = U – (U₁ + U₂ + U₃ + U₄).

Av dessa olika energivärden är U₁ lätt att
bestämma, under det att U_2, U₃ och U₄ äro svåra. Vid
goda anslag erhölls en dov ton och vid misslyckade
anslag en mera klingande ton. Vid alla försök
riktades rakbladet mot kristallens horisontella
mittlinje. Ofta följde på ett lämpligt slag en god
spaltning, ehuru kristallen ej sönderföll i två delar och
understundom blev rakbladet sittande inkilat mellan
de båda hälfterna och kunde endast efter
ansträngning dragas ut. Den nybildade spaltytan uppmättes
med mikrometer.

I förhållande till vikten A var massan hos rakbladet
så liten att energibeloppet U₄ vid
approximering kunde uteslutas. När fullständig spaltning
följer på ett slag är totala avgivna energien
U = U₀ + (U₁ + U₂ + U₃)
och när ej spaltning inträder begagnas beteckningarna
U¹ = U₁¹ + U₂¹ + U₃¹.

Av dessa två ekvationer erhålles
U₀ = (U – U¹) + (U₁¹ – U₁) + (U₂¹ – U₂) + (U₃¹ – U₃).
Om viktens förflyttning före anslaget är lika stor
så är U = U¹ och U₀= (U₁¹ – U₁ + (U₂¹ – U₂) + (U₃¹ – U₃).

Om ytterligare slaget åtföljt av spaltning och ej
åtföljt av spaltning äro fullkomligt lika, dvs. när de
giva samma ton vid anslaget och förstöra lika tjockt
lager av kristallen vid sitt inträngande bli
U₂¹ – U₂ = 0
och
U₃¹ – U₃ = 0
samt
U₀ = U₁¹ – U₁.

Under sådana betingelser skulle bestämningen av
det för spaltningen åtgångna arbetet kunna
bestämmas genom skillnaden mellan återstudsningarna.
Detta antagande är ju mycket approximativt. Vid
ett gott anslag, som följdes av god spaltning, var
studsningen minimal och vid ett dåligt anslag var
studsningen stor. Det för spaltningen åtgångna
arbetet U₀ bestämdes sedan genom följande ekvation:
U₀ = U₁¹ – U₁ = p (h₁¹ – h₁)
där h₁¹ betyder höjden, som vikten lyftes till vid
studs-ning, som åtföljde ej lyckad spaltning och h₁ höjden,
som vikten lyftes till, då den utfört lyckad spaltning.
Den specifika ytenergien bestämdes så enligt formeln

	U0
o =	––––	.
	2 F

I följande tabell finnas några försöksvärden
angivna. Om spaltningen följde efter andra slaget
infördes endast värden på o_max. Följde däremot
spaltningen först efter flera anslag, kunde man utvälja
maximala och minimala värden på h₁¹ och kunde då
angiva o_max. och o_min.

Tabell 2. Värden på specifika ytenergien på o₍₁₀₀₎
vid spaltning av koksaltkristaller efter kubytan.

Försöks- nummer	Studsning			Erhållen yta vid spaltningen 2 F	Ytenergi erg/mm2
	Maximal	Minimal	Spaltning		max.	min.
1	2,8	–	0,3	129	7	–
2	3,0	–	2,0	123	4,8	–
3	3,2	2,5	2,1	129	5,1	1,9
4	4,8	2,5	1,2	129	19,4	4,6
5	5,5	2,5	0,8	120	26,5	2,8

Då värdena på o_min torde ligga de verkliga
värdena på ytenergien närmast framgår tydligt, att Borns
värde på ytenergien för kubytan hos en
koksaltkristall 1,5 erg/mm² är av samma storleksordning
som de av Kusnezow erhållna experimentella värdena.

Kusnezow försökte även experimentellt bestämma
storleken på ytenergien utefter koksaltets
rombdodekaederyta (110). Följande tabell visar resultatet.

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>