
Full resolution (JPEG) - On this page / på denna sida - Häfte 35. 29 aug. 1942 - Problemet Sandöraset, av Ernst von Post, Arvo Ylinen, Carl Forssell, E. Nelander, Justus Österman och Ivar Häggbom
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
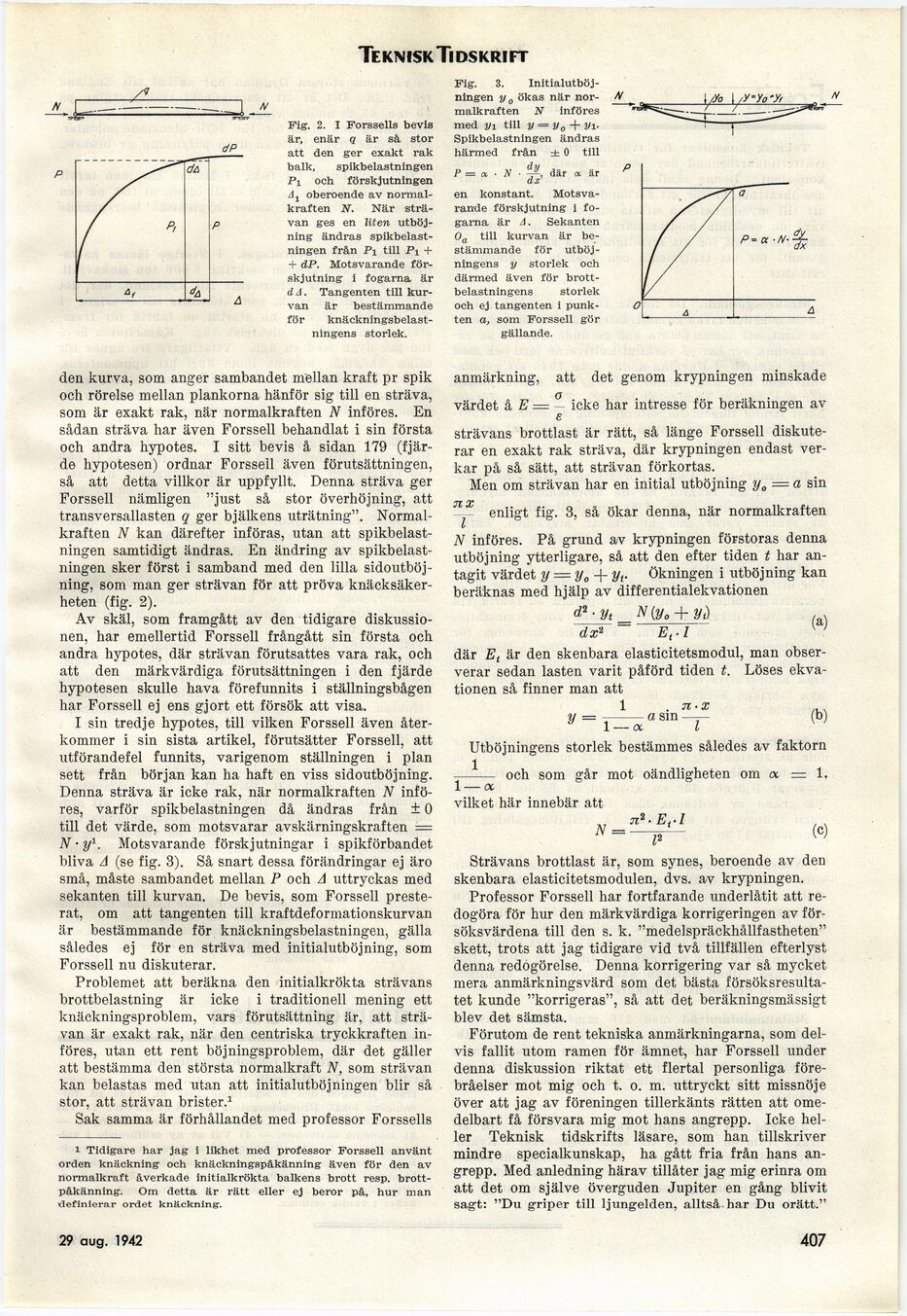
Fig. 2. I Forssells bevis
är, enär q är så stor
att den ger exakt rak
balk, spikbelastningen
Pl och förskjutningen
A j oberoende av
normalkraften N. När
strävan ges en liten
utböjning ändras
spikbelastningen från Pi till Pi +
+ dP. Motsvarande
förskjutning i fogarna är
dA. Tangenten till
kurvan är bestämmande
för
knäckningsbelast-ningens storlek.
Fig. 3.
Initialutböj-ningen y 0 ökas när
normalkraften N införes
med 3/1 till y = y0 + yj.
Spikbelastningen ändras
härmed från ± 0 till
P = » • N ■ där tx ar
dx
en konstant.
Motsvarande förskjutning i
fogarna är A. Sekanten
0a till kurvan är
bestämmande för
utböj-ningens y storlek och
därmed även för
brottbelastningens storlek
och ej tangenten i
punkten a, som Forssell gör
gällande.
den kurva, som anger sambandet mellan kraft pr spik
och rörelse mellan plankorna hänför sig till en sträva,
som är exakt rak, när normalkraften N införes. En
sådan sträva har även Forssell behandlat i sin första
och andra hypotes. I sitt bevis å sidan 179
(fjärde hypotesen) ordnar Forssell även förutsättningen,
så att detta villkor är uppfyllt. Denna sträva ger
Forssell nämligen "just så stor överhöjning, att
transversallasten q ger bjälkens uträtning".
Normalkraften N kan därefter införas, utan att
spikbelast-ningen samtidigt ändras. En ändring av
spikbelastningen sker först i samband med den lilla
sidoutböj-ning, som man ger strävan för att pröva
knäcksäkerheten (fig. 2).
Av skäl, som framgått av den tidigare
diskussionen, har emellertid Forssell frångått sin första och
andra hypotes, där strävan förutsattes vara rak, och
att den märkvärdiga förutsättningen i den fjärde
hypotesen skulle hava förefunnits i ställningsbågen
har Forssell ej ens gjort ett försök att visa.
I sin tredje hypotes, till vilken Forssell även
återkommer i sin sista artikel, förutsätter Forssell, att
utförandefel funnits, varigenom ställningen i plan
sett från början kan ha haft en viss sidoutböjning.
Denna sträva är icke rak, när normalkraften N
införes, varför spikbelastningen då ändras från ± 0
till det värde, som motsvarar avskärningskraften =
N ■ y1. Motsvarande förskjutningar i spikförbandet
bliva A (se fig. 3). Så snart dessa förändringar ej äro
små, måste sambandet mellan P och A uttryckas med
sekanten till kurvan. De bevis, som Forssell
presterat, om att tangenten till kraftdeformationskurvan
är bestämmande för knäckningsbelastningen, gälla
således ej för en sträva med initialutböjning, som
Forssell nu diskuterar.
Problemet att beräkna den initialkrökta strävans
brottbelastning är icke i traditionell mening ett
knäckningsproblem, vars förutsättning är, att
strävan är exakt rak, när den centriska tryckkraften
införes, utan ett rent böjningsproblem, där det gäller
att bestämma den största normalkraft N, som strävan
kan belastas med utan att initialutböjningen blir så
stor, att strävan brister.1
Sak samma är förhållandet med professor Forssells
i Tidigare har jag i likhet med professor Forssell använt
orden knäckning och knäckningspåkänning även för den av
normalkraft åverkade initialkrökta balkens brott resp.
brott-påkänning. Om detta är rätt eller ej beror på, hur man
definierar ordet knäckning:.
anmärkning, att det genom krypningen minskade
värdet å E = ° icke har intresse för beräkningen av
e
strävans brottlast är rätt, så länge Forssell
diskuterar en exakt rak sträva, där krypningen endast
verkar på så sätt, att strävan förkortas.
Men om strävan har en initial utböjning y0=a sin
7Z X
enligt fig. 3, så ökar denna, när normalkraften
N införes. På grund av krypningen förstoras denna
utböjning ytterligare, så att den efter tiden t har
antagit värdet y = y0-\- yt. Ökningen i utböjning kan
beräknas med hjälp av differentialekvationen
d2-yt N(y0 + y,)
dx2 E, ■ I U
där Et är den skenbara elasticitetsmodul, man
observerar sedan lasten varit påförd tiden t. Löses
ekvationen så finner man att
1 ■ 71 ’ X /UN
y = –a sm —– (b)
1 — oc t
Utböjningens storlek bestämmes således av faktorn
* och som går mot oändligheten om oc — 1,
1 — oc
vilket här innebär att
N :
ErI
l2
(c)
Strävans brottlast är, som synes, beroende av den
skenbara elasticitetsmodulen, dvs. av krypningen.
Professor Forssell har fortfarande underlåtit att
redogöra för hur den märkvärdiga korrigeringen av
försöksvärdena till den s. k. "medelspräckhållfastheten"
skett, trots att jag tidigare vid två tillfällen efterlyst
denna redogörelse. Denna korrigering var så mycket
mera anmärkningsvärd som det bästa
försöksresultatet kunde "korrigeras", så att det beräkningsmässigt
blev det sämsta.
Förutom de rent tekniska anmärkningarna, som
delvis fallit utom ramen för ämnet, har Forssell under
denna diskussion riktat ett flertal personliga
förebråelser mot mig och t. o. m. uttryckt sitt missnöje
över att jag av föreningen tillerkänts rätten att
omedelbart få försvara mig mot hans angrepp. Icke
heller Teknisk tidskrifts läsare, som han tillskriver
mindre specialkunskap, ha gått fria från hans
angrepp. Med anledning härav tillåter jag mig erinra om
att det om själve överguden Jupiter en gång blivit
sagt: "Du griper till ljungelden, alltså har Du orätt."
19 sept. 1942
407
<< prev. page << föreg. sida << >> nästa sida >> next page >>