
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
TekniskTidskrift
+ (6 + /’ 2) (—5 4-/3) + (12 + /4) (3-/2)] :
: (28 + /4) =34-/4;
Vo = [214 4-/12 — (4 4-/2) (6 — / 5) +
+ (8 + /’ 4) (— 5 4-/3) — (8 4- /4) (4 4/2)] :
: (16 + /8) = — 9 — / 3.
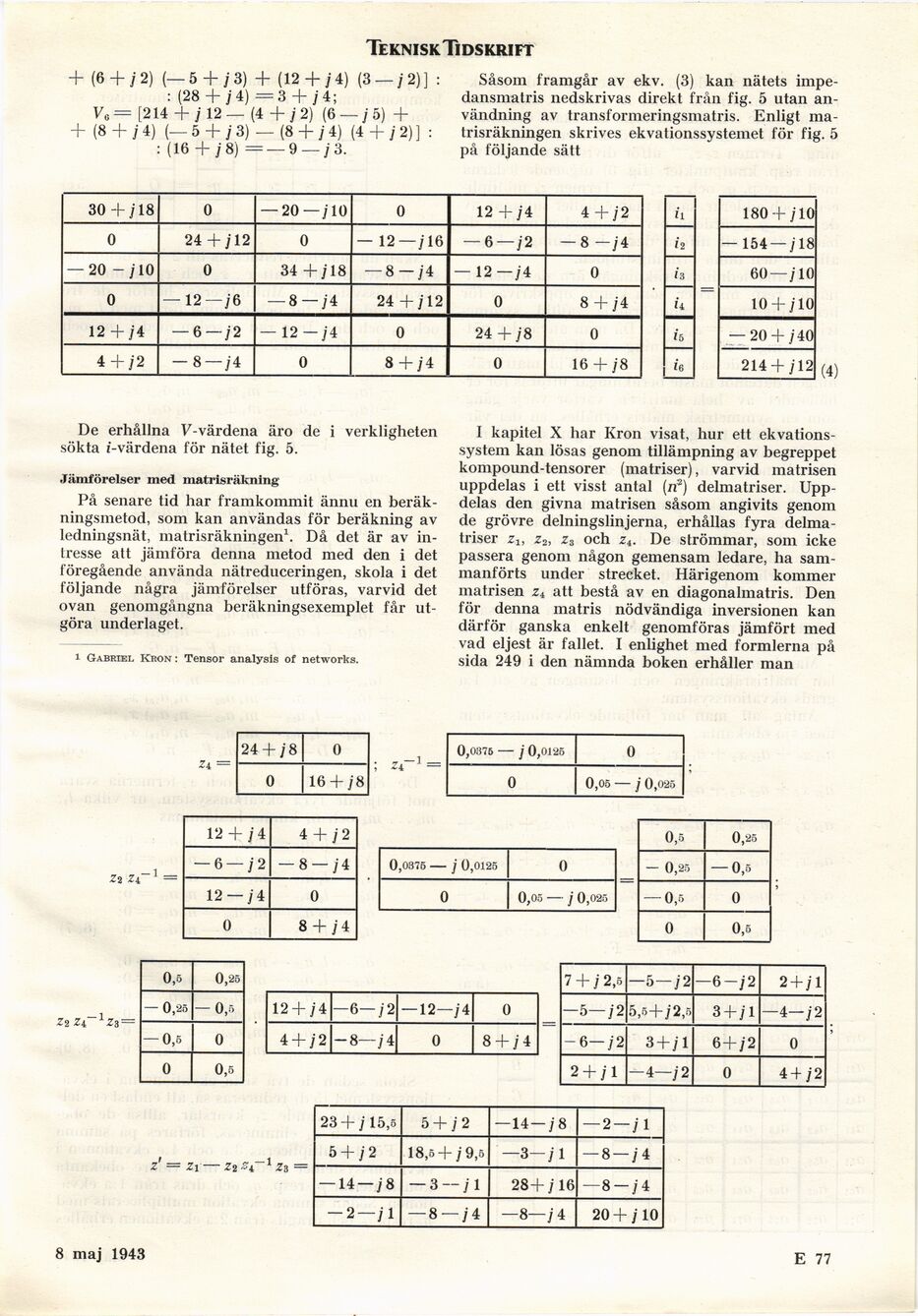
Såsom framgår av ekv. (3) kan nätets
impedansmatris nedskrivas direkt från fig. 5 utan
användning av transformeringsmatris. Enligt
matrisräkningen skrives ekvationssystemet för fig. 5
på följande sätt
30 + /18 0 — 20—/10 0 12+/4 4 + / 2
0 24 4- /12 0 - 12—/16 -6-/2 — 8 —/4
-20-/10 0 34 +/18 -8-/4 -12-/4 0
0 -12—/6 -8-/4 24 4- /12 0 8 + /4
12+/4 -6-/2 - 12 — / 4 0 24 + / 8 0
4 +/2 — 8-/4 0 8 + /4 0 16 + /8
ii 180 4-/10
«2 — 154 — /18
/3 60 — /10
ii 10 + /10
ib — 20 + /40
t. 214 + /12
(4)
De erhållna V-värdena äro de i verkligheten
sökta i-värdena för nätet fig. 5.
Jämförelser med matrisräkning
På senare tid har framkommit ännu en
beräkningsmetod, som kan användas för beräkning av
ledningsnät, matrisräkningen1. Då det är av
intresse att jämföra denna metod med den i det
föregående använda nätreduceringen, skola i det
följande några jämförelser utföras, varvid det
ovan genomgångna beräkningsexemplet får
utgöra underlaget.
i Gabriel Kron : Tensor analysis of networks.
I kapitel X har Kron visat, hur ett
ekvationssystem kan lösas genom tillämpning av begreppet
kompound-tensorer (matriser), varvid matrisen
uppdelas i ett visst antal (lf) delmatriser.
Uppdelas den givna matrisen såsom angivits genom
de grövre delningslinjerna, erhållas fyra
delmatriser Zi, z2, z3 och z4. De strömmar, som icke
passera genom någon gemensam ledare, ha
sammanförts under strecket. Härigenom kommer
matrisen zé att bestå av en diagonalmatris. Den
för denna matris nödvändiga inversionen kan
därför ganska enkelt genomföras jämfört med
vad eljest är fallet. I enlighet med formlerna på
sida 249 i den nämnda boken erhåller man
Zi
24 + / 8 0
0 16 4-/8
; Zi 1 =
0,0376 — / 0,0125 0
0 0,05 — / 0,025
Zi Zi
12 + / 4 4 + / 2
— 6 — / 2 — 8 — / 4
12—/ 4 0
0 8 + / 4
0,5 0,25
0,0375 — / 0,0125 0 - 0,25 — 0,5
0 0,05 — / 0,025 -0,5 0
0 0,6
Zi Zi 1Za-
0,5 0,25
— 0,25 — 0,5
— 0,5 0
0 0,5
7 + / 2,5 —5-/2 —6-/2 2 + /1
12 4-/4 -6-/2 —12—/4 0 -5-/2 5,5 + /2,6 34-/1 -4-/2
4 + /2 -8-/4 0 8 + / 4 -6-/2 3 + /1 6 + /2 0
2 + /1 —4—/2 0 4+ / 2
z = Zi-
■ Zi%i 1 z3 =
23 + /15,5 5 + /2 — 14— / 8 -2-/1
5 + / 2 18,5 + /9,6 -3-/1 -8-/4
—14 — / 8 -3-/1 28+ / 16 -8-/4
-2-/1 -8-/4 —8-/4 20 + /10
8 maj 1943
E 77
<< prev. page << föreg. sida << >> nästa sida >> next page >>