
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
50
TEKNISK TIDSKRIFT
16 FEBR. 1929
Denna i och för sig utomordentligt höga
noggrannhet är dock icke tillräcklig om man vill använda
passbitarna såsom prototyper. Härvid måste man,
för att få ett exakt värde på passbitens absoluta
längd använda sig av betydligt finare
mätningsmetoder. Sådana hava vi i den s. k. interferensmetoden,
dvs. vi kunna, genom att fastställa huru många
ljusvågor av en viss våglängd som falla på en viss
passbits längd noggrant bestämma dess absoluta längd
uttryckt i ljusvåglängder.
Teoretiskt sett skulle således, under förutsättning
av att noggranna instrument stode till buds för
mätning av dessa ljusvåglängder, en absolut bestämning
av passbitens längd vara en jämförelsevis enkel
procedur. Det är dock en hel del faktorer som
komplicera denna procedur och med vilka vi i det följande
skola sysselsätta oss. I trots av att man kan
bestämma en passbits absoluta längd med en säkerhet
av 0,01—0,02 fi, så bjuder försiktigheten att inte gå
längre i garanti än till 0,05 + 0,15 • 10—5 av dess längd,
dvs. för en 100 mm passbit skulle man således med
säkerhet kunna giva en garanti för att det absoluta
måttet innehålles inom gränserna av 0,2 För
passbitar, vilka användas för jämförande mätningar
enligt interferensmetoden är denna noggrannhet icke
tillräcklig. Det möter dock som sagt ingen svårighet
att kunna bestämma prototypers absoluta längd inom
gränserna av 0,01—0,02 u. dock erfordras härför lång
övning och vana samt en utsökt apparatur, varför
sådana ytterligt noggranna mätningar endast kunna
utföras i de härför inrättade vetenskapliga
laboratorierna. (Exempelvis Physikalisch-Technische
Reichsanstalt für Masse und Gewicht, Berlin.)
I det följande skola vi sysselsätta oss med att söka
giva en inblick i huru dessa mätningar kunna
utföras så att säga rent verkstadsmässigt, dvs. med
sådana resurser som kunna tänkas vara tillgängliga
för ett väl inrett verkstadslaboratorium, nota bene vid
sådana verkstäder, där man har intresse av denna
höga noggrannhet, exempelvis fabrikanter, av
noggranna mätverktyg m. fi.
Kontrollering av ändmått (passbitar) enligt
interferensmetoden.
En passbit måste kontrolleras med avseende på
mätytornas planhet, parallellitet och exakta avstånd.
a) Kontrollering av ändytornas planhet.
För kontrollering av ändytornas planhet vid en
passbit betjänar man sig av ett s. k. planglas, dvs.
en av optiskt glas bestående noggrant planslipad
glasplatta av 10—15 mm tjocklek. Lägges detta
planglas på mätytan, så uppstå s. k. interferenslinjer
som en följd av den olikformiga tjockleken av
luftskiktet mellan glasplatta och mätyta. Av formen och
antalet av dessa interferenslinjer kan man sluta sig
till mätytans planhet. För att förstå detta, torde det
vara nödvändigt att något närmare ingå på teorien
för uppkomsten av dessa ljusfenomen.
Ljusets fortplantning i etern sker i vågrörelse.
Samverkan av två eller flera vågor kallas interferens.
Det första ljusfenomen, som blev förklarat som
beroende av ljusets interferens, var det vackra
färgspel, som man iakttager i tillräckligt tunna skikt
(lameller) av ett genomskinligt ämne, t. e. en
såpbubbla, eller olja på vatten. Lägger man en svagt
konvex lins på en plan glasskiva, så uppkomma i
det tunna luftskiktet mellan glasskivorna,
mång-färgade ringar, de s. k. Newtonska ringarna, vilka
äro beroende av ljusets interferens. Detsamma gäller
även om ett par plana glasskivor läggas uppå
varandra och utefter ena sidan lägges ett stycke tunt
papper, så att ett kilformigt luftskikt bildas emellan
dem, varvid interferenslinjerna löpa parallellt med
kilspetsen.
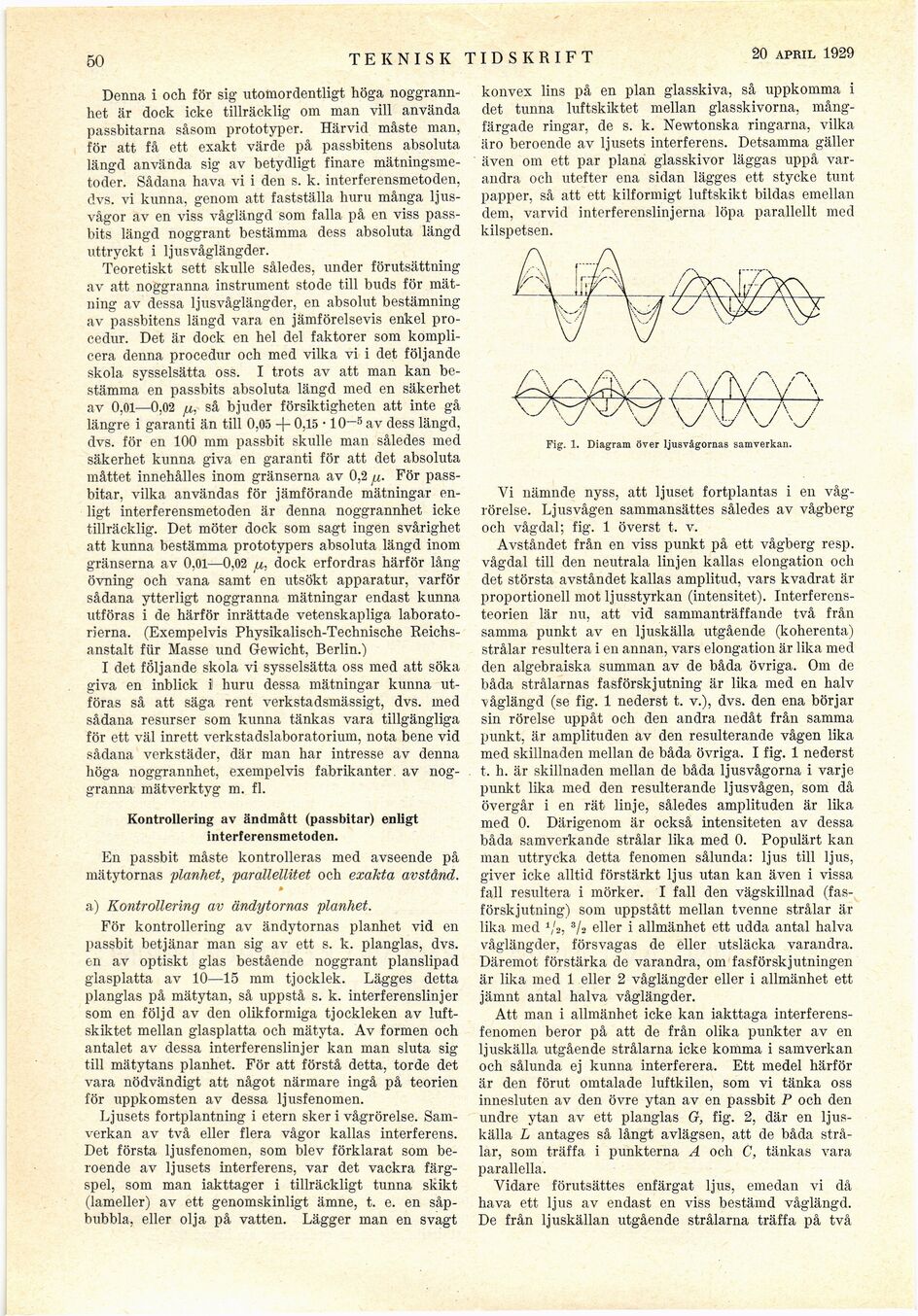
•1/ \y W
Fig. 1. Diagram över ljusvågornas samverkan.
Vi nämnde nyss, att ljuset fortplantas i en
vågrörelse. Ljusvågen sammansättes således av vågberg
och vågdal; fig. 1 överst t. v.
Avståndet från en viss punkt på ett vågberg resp.
vågdal till den neutrala linjen kallas elongation och
det största avståndet kallas amplitud, vars kvadrat är
proportionell mot ljusstyrkan (intensitet).
Interferens-teorien lär nu, att vid sammanträffande två från
samma punkt av en ljuskälla utgående (koherenta)
strålar resultera i en annan, vars elongation är lika med
den algebraiska summan av de båda övriga. Om de
båda strålarnas fasförskjutning är lika med en halv
våglängd (se fig. 1 nederst t. v.), dvs. den ena börjar
sin rörelse uppåt och den andra nedåt från samma
punkt, är amplituden av den resulterande vågen lika
med skillnaden mellan de båda övriga. I fig. 1 nederst
t. h. är skillnaden mellan de båda ljusvågorna i varje
punkt lika med den resulterande ljusvågen, som då
övergår i en rät linje, således amplituden är lika
med 0. Därigenom är också intensiteten av dessa
båda samverkande strålar lika med 0. Populärt kan
inan uttrycka detta fenomen sålunda: ljus till ljus,
giver icke alltid förstärkt ljus utan kan även i vissa
fall resultera i mörker. I fall den vägskillnad
(fasförskjutning) som uppstått mellan tvenne strålar är
lika med 1/2, eller i allmänhet ett udda antal halva
våglängder, försvagas de eller utsläcka varandra.
Däremot förstärka de varandra, om fasförskjutningen
är lika med 1 eller 2 våglängder eller i allmänhet ett
jämnt antal halva våglängder.
Att man i allmänhet icke kan iakttaga
interferensfenomen beror på att de från olika punkter av en
ljuskälla utgående strålarna icke komma i samverkan
och sålunda ej kunna interferera. Ett medel härför
är den förut omtalade luftkilen, som vi tänka oss
innesluten av den övre ytan av en passbit P och den
undre ytan av ett planglas G, fig. 2, där en
ljuskälla L antages så långt avlägsen, att de båda
strålar, som träffa i punkterna A och C, tänkas vara
parallella.
Vidare förutsättes enfärgat ljus, emedan vi då
hava ett ljus av endast en viss bestämd våglängd.
De från ljuskällan utgående strålarna träffa på två
<< prev. page << föreg. sida << >> nästa sida >> next page >>