
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Mekanik.
Lerans underyta betraktas som fast.
I detta fall tages lerans underyta till 2r?/-plan och
z-axeln vertikalt uppåt.
I detta axelsystem blir fundamentallösningen,
motsvarande en koncentrerad, nedåtriktad enhetskraft
i punkten z—p och förskjutningsfri underyta:
där z—c är pålens undre spets. Ur denna ekv. fås
f 2 , (g - c) (l + c —z)
x{z) = yJy-^{z) — r{z)\ogK–; -
w
-4
x2 -f- y2
+ 4
N ’
p z
+ -
x2 -)- y2
l+c
J \P— *
l + c
dp +
*(P)
p-\-z
dp -f-
N3 1 M
pz x2 -f 2/2
A/3
+
2 + c
-6
5 J.
/ M3 " y M5
där /Ë, a och y ha samma betydelse som ovan.
Ur en analog integralekvation och efter
gränsövergång till försvinnande r i likhet med föregående fall,
erhålles den mot (4) svarande ekv.
där
+ å* fö^adp) +K+co2JdC (t{P)dp, (5’)
C C C
2 (* + /u)
å =
(A + 2 /»)(!
H-8/t)-En serieutveckling efter x ger slutligen som andra
approximation
t(2)(z) = K ch co(z — c) -f 14 (log CO l -f C+ ch
m[z — c)
+ <5
2 ø
-C-{-g (c + g)2 \l+c + g) (l+c + z)2
ch coZ +
coz’
1 + c-\g
sh co l
—c)
[Ei(- co[z—c)) +
+ Ei(co(Z+c— *))] — e~ra(*~c)[Ei — c))-f Ei(— oi{l-\- c — g))] +
j y-°°(.c+*)[Ei{æ(i+c+z))_ Ei(0)(c + 2)) j +
",(e+’)[Ei(-a»(i + p-\- z))-Ei(— co(c + *))]
+
cozl 1 -
+ [l-ycoz 1 +
toz
coz
(’V)
■ ocx (z) log
4 Z2 (z — c) (Z + c — 2)
+ 2r(z) —
J p-S ^ J p + *
l+c
+ 4
v Av)
r J [p + z†
dp
}-
konst.-
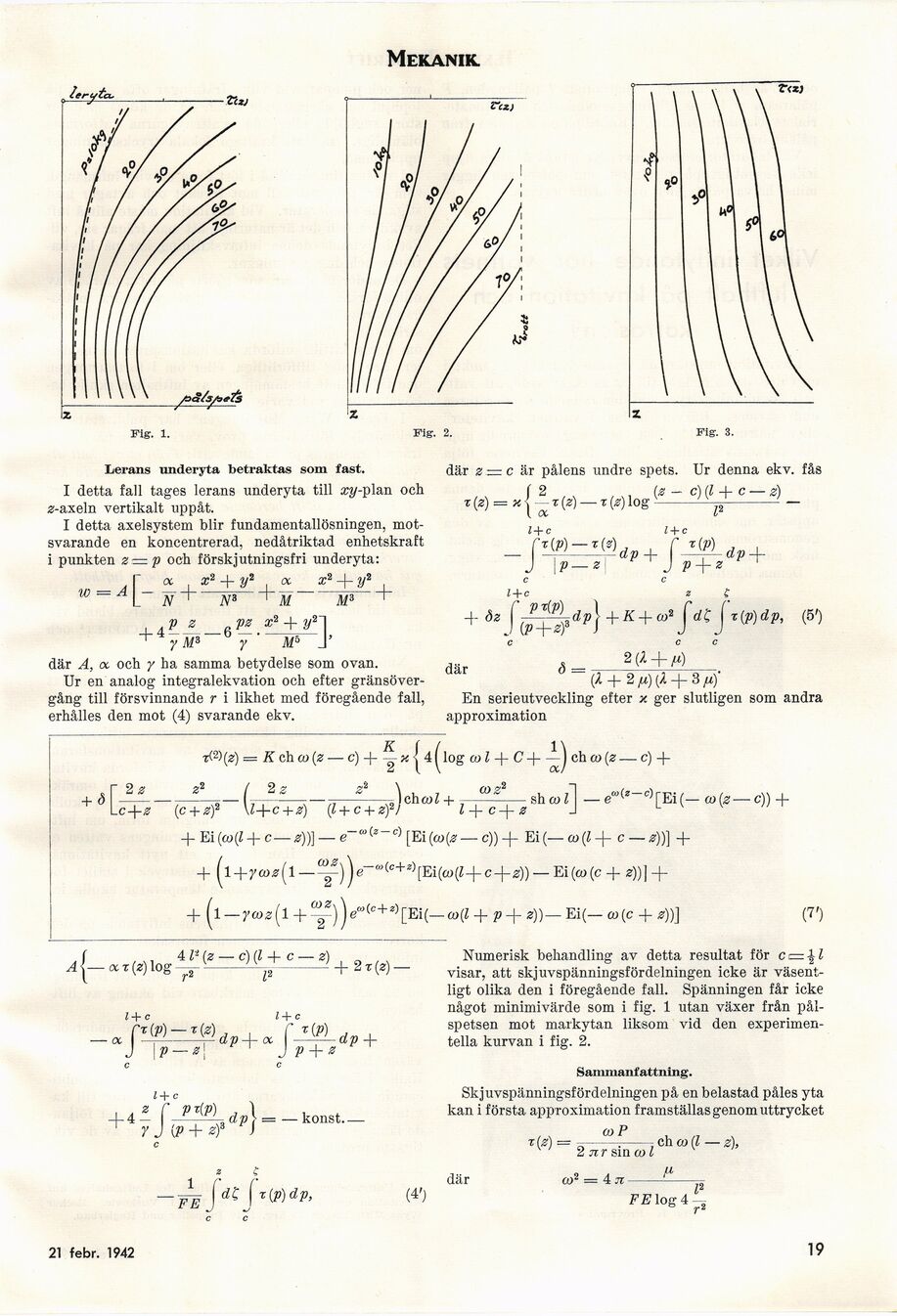
Numerisk behandling av detta resultat för c = -|Z
visar, att skjuvspänningsfördelningen icke är
väsentligt olika den i föregående fall. Spänningen får icke
något minimivärde som i fig. 1 utan växer från
pål-spetsen mot markytan liksom vid den
experimentella kurvan i fig. 2.
Sammanfattning.
Skjuvspänningsfördelningen på en belastad påles yta
kan i första approximation framställas genom uttrycket
coP
r (g):
2 nr sin co l
ch co (l — z),
z i
- — JdCjr(p)dp,
(4’)
där
CO2 = 4 JT
FE log 4
21 febr. 1942
19
<< prev. page << föreg. sida << >> nästa sida >> next page >>