
Full resolution (TIFF) - On this page / på denna sida - Vankant ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
f &<^eu^l&**x
1161
variation beror på rent tillfälliga orsaker,
såsom olika klimat, jordmån, växtplats o. s. v.,
eller, då det gäller djur, olika uppfödning, vård
o. s. v. och är betingad av växt- och
djurindividens förmåga att anpassa sig efter
förhandenvarande levnadsbetingelser (se Acklimatisering).
De av dylika tillfälliga orsaker framkallade
avvikelserna, man kallar dem
modifikationer, tillhöra s. k. förvärvade
egenskaper och äro såsom sådana, efter
vad man hittills vet, icke ärftliga. Bestämt
förneka möjligheten av förvärvade egenskapers
ärftlighet kan man dock icke, men man känner
hittills icke något säkert bevisat fall av dylik.
Mäta vi exempelvis planthöjden hos de
enskilda plantorna i ett bestånd av en fullt
enhetlig sädessort, t. ex. Prinsesskorn, vars alla
individ äro ärftligt lika, tillhöra samma biotyp
(se Ärftlighet), och beräkna vi med ledning
därav även hela beståndets medelplanthöjd,
skola vi finna, att flertalet plantor mer eller
mindre närma sig denna, medan de övriga
såsom plus- (högre) och minus- (lägre)
modifikationer fördela sig i
kontinuerliga serier med ungefär lika antal på ömse
sidor och med ett jämväl å båda sidor på
ungefär samma sätt utåt småningom avtagande
individantal. Vid närmare undersökning visar
sig individens fördelning nära
överensstämma med den talserie, som erhålles vid
utveckling av den s. k. binominalformeln
(a + &)*, då både a och b sättas lika med i,
»Quetelets lag», efter belgiske antropologen
Quetelet, som först påvisade denna
överensstämmelse. Ett enkelt och praktiskt sätt att
utveckla formeln (i + i)« och att sålunda finna
den därav framgående talserien visar följande
schema:
(i 4 i)1 = I + I = 2
(i + l)a = I 4- 2 4- I = 4
(i + i)* ~ i +T^~T+ i = 8
(i + i)* = i 4- 4 4- 6 + 4 + i ■ = 16
(i 4- i)5 = I 4- ^ 4- IO 4- IO 4- 5 4- I =32
(i 4- i)10 = I 4- IO 4- 45 4- I20 4- 2IO 4-
252 + 2IO 4- 120 + 45 4- IO 4- I = 1,024
Den binominala talserien liksom vilken
variationsserie som helst kan man framställa
grafiskt i form av en kurva, såsom följande
figur närmare åskådliggör, visande variationen
i längd hos ett antal bönor (efter Johannsen).
Vi ha här att göra med s. k.
klassvarianter, då alla möjliga övergångar finnas mellan
de olika variantklasserna: 17, 19, 21 o. s. v.
mm., såsom ju alltid måste bliva fallet, då
skillnaderna äro liktydiga med ett mer eller
mindre, med olika grader av en egenskap.
Individens antal är i detta fall angivet genom
rektanglar, vilkas höjd och sålunda även
storlek står i direkt förhållande till antalet individ
inom resp. variantklasser. En sådan figur
kallas p o 1 y g o n, och motsvarande kurva
erhålles helt enkelt genom att sammanbinda
mittpunkterna i rektanglarnas övre
horisontala linjer. Kurvan är här icke inritad, men
man ser genast, att den skulle nära
överensstämma med den i stället inritade ideala
eller binominala
variationskurvan, även kallad slumpkurva. Har
man däremot att göra icke med klass varianter
utan i stället med s. k. diskreta varian-
1? /†
sj 53 15 a?
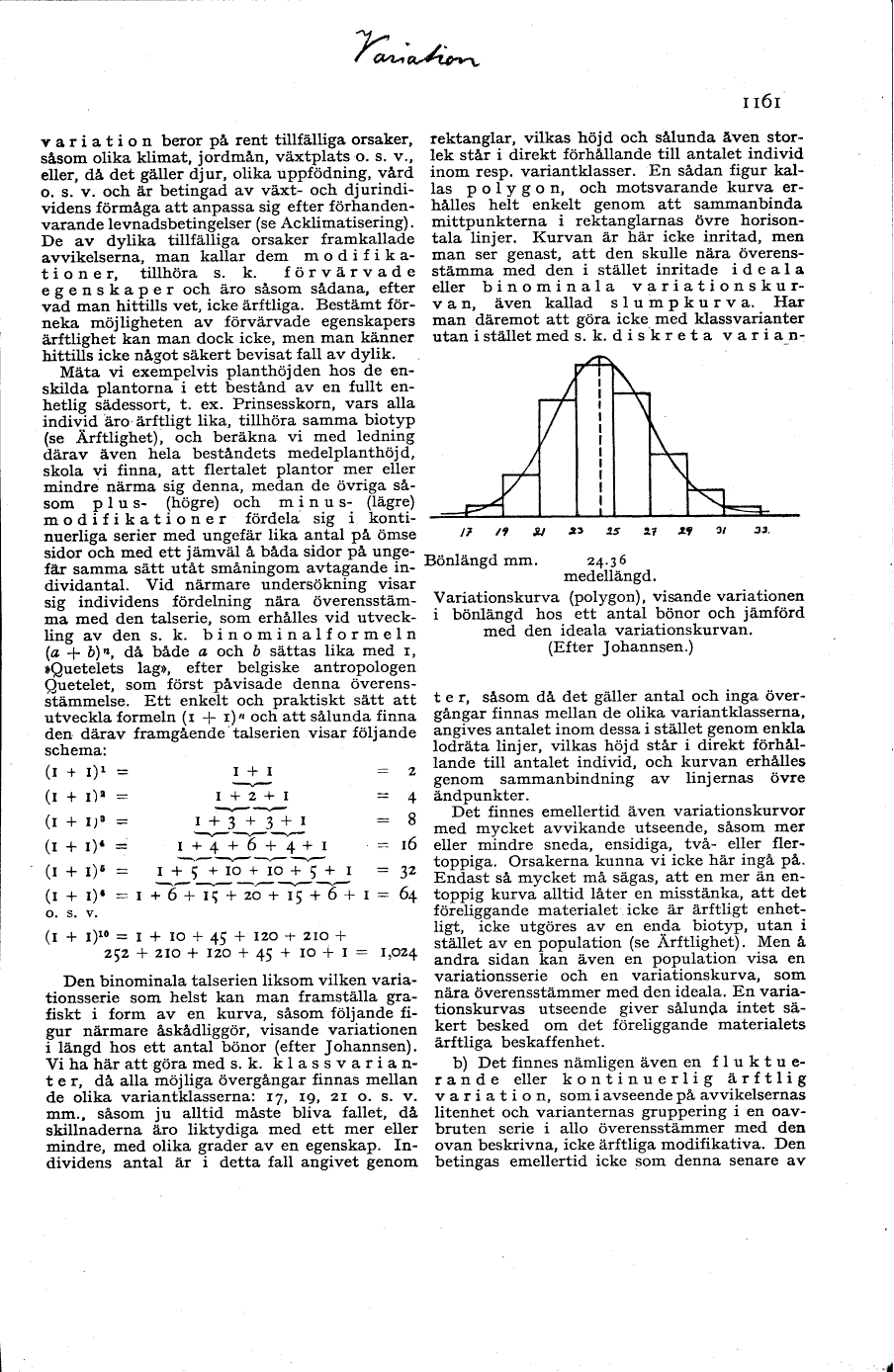
Bönlängd mm. 24.36
medellängd.
Variationskurva (polygon), visande variationen
i bönlängd hos ett antal bönor och jämförd
med den ideala variationskurvan.
(Efter Johannsen.)
ter, såsom då det gäller antal och inga
övergångar finnas mellan de olika variantklasserna,
angives antalet inom dessa i stället genom enkla
lodräta linjer, vilkas höjd står i direkt
förhållande till antalet individ, och kurvan erhålles
genom sammanbindning av linjernas övre
ändpunkter.
Det finnes emellertid även variationskurvor
med mycket avvikande utseende, såsom mer
eller mindre sneda, ensidiga, två- eller
fler-toppiga. Orsakerna kunna vi icke här ingå på.
Endast så mycket må sägas, att en mer än
en-toppig kurva alltid låter en misstänka, att det
föreliggande materialet icke är ärftligt
enhetligt, icke utgöres av en enda biotyp, utan i
stället av en Population (se Ärftlighet). Men å
andra sidan kan även en Population visa en
variationsserie och en variationskurva, som
nära överensstämmer med den ideala. En
variationskurvas utseende giver sålunda intet
säkert besked om det föreliggande materialets
ärftliga beskaffenhet.
b) Det finnes nämligen även en
fluktuerande eller kontinuerlig ärftlig
variation, som i avseende på avvikelsernas
litennet och varianternas gruppering i en
oavbruten serie i allo överensstämmer med den
ovan beskrivna, icke ärftliga modifikativa. Den
betingas emellertid icke som denna senare av
<< prev. page << föreg. sida << >> nästa sida >> next page >>