Handledning uti nivelleringskonsten / 4-5 (1853) Author: Adolf Helander Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (JPEG) - On this page / på denna sida - §. 2. Allmänna begrepp - §. 3. Beräkning af korrektionen för jordens rundning

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

En sådan horizontal-linie, som den omnämnda, kallas verklig
till skillnad från skenbar horizontal-linie, hvilken sednare
tangerar den förra i dess ena ända (observatorns ståndpunkt). Denna
tangent ab, som är en rät linie och vinkelrät mot vertikal-linien i
observatorns ståndpunkt, afviker från jordytan eller från den
verkliga horizontal-linien i mon som afståndet från observatorns
ståndpunkt a tilltager; hvaraf följer, att hvarje ställe på jordytan måste
hafva sin egen skenbara horizont och att dessa horizontal-linier
icke kunna vara parallela med hvarandra. Skulle bågen aa endast
vara omkring 300 fot lång åt hvardera sidan från en punkt a, så
kan man i praktiken utan märkligt fel anse den skenbara och
verkliga horizontal-linien sammanfalla, och behöfver således någon
korrektion ej komma i fråga för en distance om 300 alnars längd.
Skulle åter den afvägda distancen vara större än 300 alnar bör
korrektion företagas på sätt nedan kommer att visas.

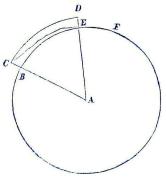Fig. 2.

Emedan vattnet uti hafvet, sjöar och andra stillastående
vatten, icke kan, enligt tyngdens verkan, vara i jemnvigt, om ej hvarje
punkt på ytan vore lika långt från jordens medelpunkt, så kallas
äfven en sådan linie som BEF (fig. 2) för en vågrät linie,
vattenpass-linie och vatten-horizont; och alla de ställen sägas vara
i vattenpass (au niveau) med hvarandra, som ligga lika långt från
jordens medelpunkt, hvilken således är normal-punkten för ställens
ifrågavarande böjdbestämmelse. För lättare jemförelse mellan mera
aflägsne orter brukar man hänföra dem till hafsytan och beräkna
deras olika höjd öfver denna, då således jordradierne från ytan till
medelpunkten, såsom lika stora, ej behöfva komma i beräkning.
Skulle man å fig. 2 önska känna höjdskillnaden mellan C och E,
så föreställer man sig tvänne verkliga horizontal-linier beskrifna
genom dessa punkter, neml. BE och CD, då den vinkelräta linien
BC utvisar höjdskillnaden eller huru mycket C ligger öfver E, och
är det alltså denna linie, som man medelst afvägning söker
bestämma.

Man kallar hvarje ställe, der man vid en afvägning uppställer
instrumentet för att dermed operera, för station; stationens
ändpunkter, hvilkas höjdskillnad man söker, kallas distance-punkter,
afvägnings-punkter eller termer. Den punkt, hvarmed
afvägningen börjar, utgör den första termen, och den, hvarmed den slutar,
kallas den sista termen.

I afseende å utöfningen är sjelfva afvägningen antingen Enkel
eller Sammansatt. Enkel afvägning kallas en sådan, som kan
verkställas med en enda station, och sammansatt afvägning den,
hvartill flera stationer erfordras. Afvägnings-operationen, enkel eller
sammansatt, verkställes, allt efter markens olika beskaffenhet,
antingen från någondera ändpunkten, eller från midten af
stationslängderna.

§. 3.

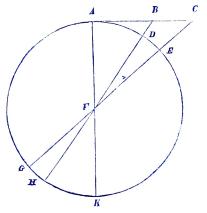Fig. 3.

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>