Handledning uti nivelleringskonsten / 116-117 (1853) Author: Adolf Helander Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (JPEG) - On this page / på denna sida - §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

tangenten, man då medelst ett reflektions-instrument, t. ex. en
spegelsextant, hvilken ställes så, att den innefattar vinkeln BDF, äfven
kan finna nödigt antal punkter i kurven mellan D och B.
Emedan uti ett ock samma cirkel-segment alla periferi-vinklar, hvilkas
vinkelben sluta i ändpunkterna af kordan äro lika stora, så följer
deraf och af det föregående, att hvarje instrumentets station mellan
punkterna B och D, der dessa begge punkter täcka hvarandra i
instrumentets spegel, måste ligga i den åstundade kurven, och att
man genom ett uti en tråd från instrumentet hängande lod således noga
kan bestämma de punkter, genom hvilka kurven skall gå. För att
kunna afsticka kurver efter denna method är likväl nödigt att finna
en kordas längd i anseende till vinkeln, som densamma gör emot
tangenten, eller omvändt, beräkna denna vinkel, då kordans längd
är känd.

Kordans längd är, då radien antages till 1, lika med dubbla
sinus för den tillhörande halfva centri-vinkeln. Då nu vinkeln
EDB, som BD bildar mot tangenten ED, är lika stor med
periferi-vinkeln BCD, men denna åter är lika med halfva centri-vinkeln, så
är kordan DB = dubbla sinus för vinkeln EDB, eller, då radien
sättes = r, = 2r . sin. EDB; och altså sin. EDB = DB / 2r eller ¹/₂DB / r.

För att spara besväret att på fältet anställa beräkningarne,
kan man på förhand upprätta tabeller, som för alla brukliga radier
upptaga kordans storlek äfvensom vinkeln, som denna sednare gör
mot tangenten.

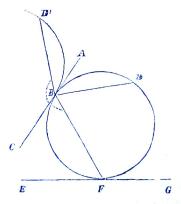Fig. 55.

I fig. 55 antages FG motsvara jernbanans räta direktlon, och
alt från punkten F en kurv skulle beskrifvas med 5280 fots lång
radie. Man uppställer då en theodolit i punkten F och väljer en
korda, så lång, som t. ex. terrainen tillåter. Antag denna till
199,6’, så får man vinkeln, som den skärande linien gör mot
tangenten EF, eller vinkeln EFB, ur förut angifna formel för kordans
storlek, eller FB = 2r . sin. y;

altså sin. y =	FB / 2r eller med logarithmer:
log. sin. y (EFB) =	log.		199,6 —	log. 10560 + log. R
log. sin. EFB =	{	log. + log.	199,6 = R =	2.3001605 10
–––––––––––––––––––––––––
				12.3001605
— log.			10560 =	4.0236639
–––––––––––––––––––––––––––––
log. sin. EFB =				8.2764966

                                                                Λ EFB = 1°5’ (då ej
sekunder beräknas), och således supplement-vinkeln BFG (= 180°
— 1°5’)= 178°55’. Man låter nu theodoliten visa denna vinkel
om 178°55’ och uppmäter derefter FB = 199,6 fot. Efter det nu
en signal i B blifvit noga inriktad enligt hårkorset i tuben,
borttager man theodoliten från F och uppställer der äfven en signal.
Nu upptager man i spegel-sextanten en vinkel om 178°55’, och
går med instrumentet framåt i kurvens ungefärliga riktning, så långt
som behöfves emellan första och andra punkten i kurven, hvarefter
man syftar genom okular-öppningen på instrumentets spegel, och
ändrar så ofta plats, intilldess den ena utsatta stången (signalen)
sammanfaller med spegelbilden af den andra, då lodet vid
instrumentet noga anger kurv-punkten. På enahanda sätt fortfar man
hela vägen intilldess man erhållit så många punkter, som nödiga
äro. Sedan man afstuckit kurven till B, så borttager man
signalstången i denna punkt och uppställer der theodoliten samt
bestämmer, i förhållande till terrainens beskaffenhet och den längd, man
vill gifva åt kurven, nästa kördas längd, låt vara t. ex. 396’, så
finner man då, att, med bibehållande af ofvan antagna radie,
motsvarande vinkeln mot tangenten är, i det närmaste, 2°9’, och
således supplement-vinkeln 177°51’. Bäst är att bestämma den
andra kordans riktning genom vinkel-afsättande ifrån den förra.
Denna vinkel erhålles sålunda, att, emedan vinkeln CBF är = EFB och
FBD är = CBD — CBF, eller, som är detsamma = CBD - EFB, så
erhålles denna vinkel FBD, om man från den trubbiga vinkel, som

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>