
Full resolution (TIFF) - On this page / på denna sida - Elfte Boken. VI Proposition. Theorem - Elfte Boken. VII Proposition. Theorem - Elfte Boken. VIII Proposition. Theorem
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
244
Elfte Boken.
Elfte Boken.
245
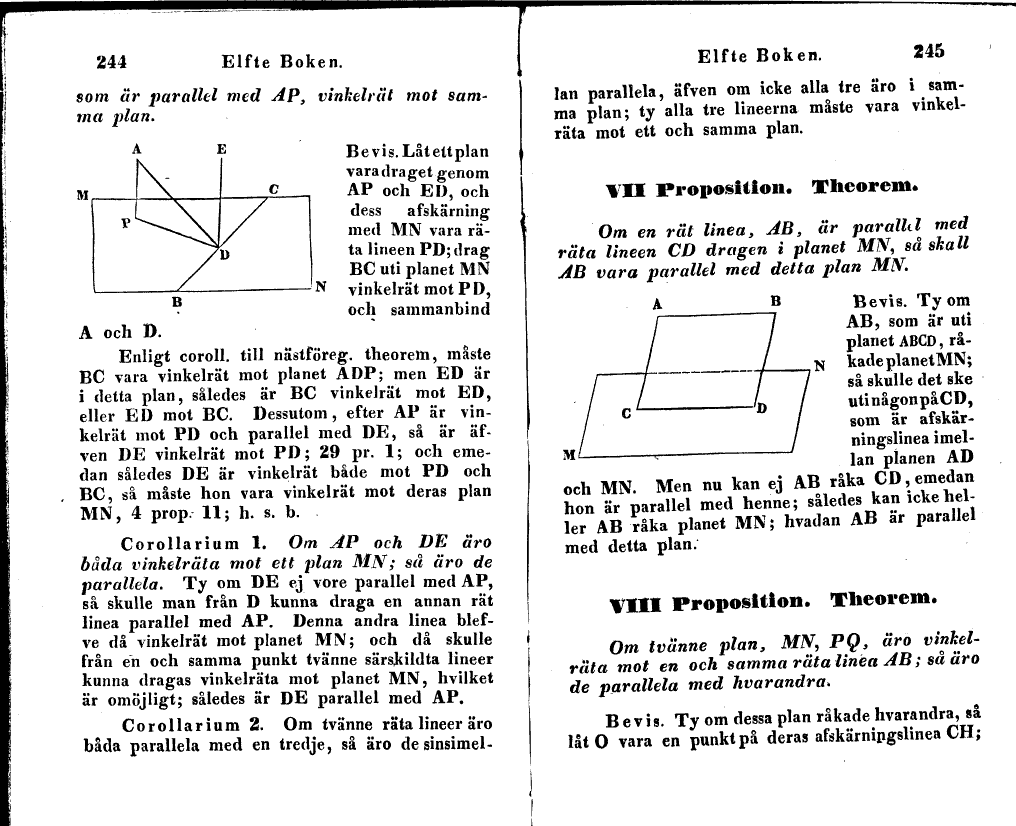
som är parallel med AP, vinkelrät mot samma plan.
Bevis.Låtettplan vara draget genom AP och ED, och dess
afskärning med M1V vara räta lineen PD; drag BC uti
planet MN vinkelrät mot P D, och sammanbind A och D.
Enligt coroll. till nastföreg. theorem, måste BC
vara vinkelrät mot planet ADP; men ED är i detta
plan, således är BC vinkelrät mot ED, eller ED
mot BC. Dessutom, efter AP är vinkelrät mot PD och
parallel med DE, så är äfven DE vinkelrät mot PD; 29
pr. 1; och emedan således DE är vinkelrät både mot PD
och BC, så måste hon vara vinkelrät mot deras plan MN,
4 prop. 11; h. s. b.
Corollarium 1. Om AP och DE äro
båda vinkelräta mot ett plan MN; sä äro de
parallela. Ty om DE ej vore parallel med AP, så skulle
man från D kunna draga en annan rät linea parallel
med AP. Denna andra linea blefve då vinkelrät mot
planet MN; och då skulle från en och samma punkt
tvänne särskildta lineer kunna dragas vinkelräta mot
planet MN, hvilket är omöjligt; således är DE parallel
med AP.
Corollarium 2. Om tvänne räta lineer äro båda
parallela med en tredje, så äro de sinsimel-
lan parallela, äfven om icke alla tre äro i samma
plan; ty alla tre lineerna måste vara vinkelräta mot
ett och samma plan.
VII Proposition. Theorem.
Om en rät linea 9 AB, är parallel med räta lineen
CD dragen i planet MN, så skall AB vara parallel med
detta plan MN.
Bevis. Ty om AB, som är uti planet ABCD, rått kade
planet MN; så skulle det ske utinågonpåCD, som är
afskär-ningslinea imellan planen AD och MN. Men nu
kan ej AB råka CD, emedan hon är parallel med henne;
således kan icke heller AB råka planet MN; hvadan AB
är parallel med detta plan.
VIII Proposition» Theorem.
Om tvänne plany MN, PQ, äro vinkelräta mot en
och samma räta linea AB; så äro de parallela med
hvarandra.
Bevis. Ty om dessa plan råkade hvarandra, så låt O
vara en punkt på deras afskärnipgslinea CH;
<< prev. page << föreg. sida << >> nästa sida >> next page >>