
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
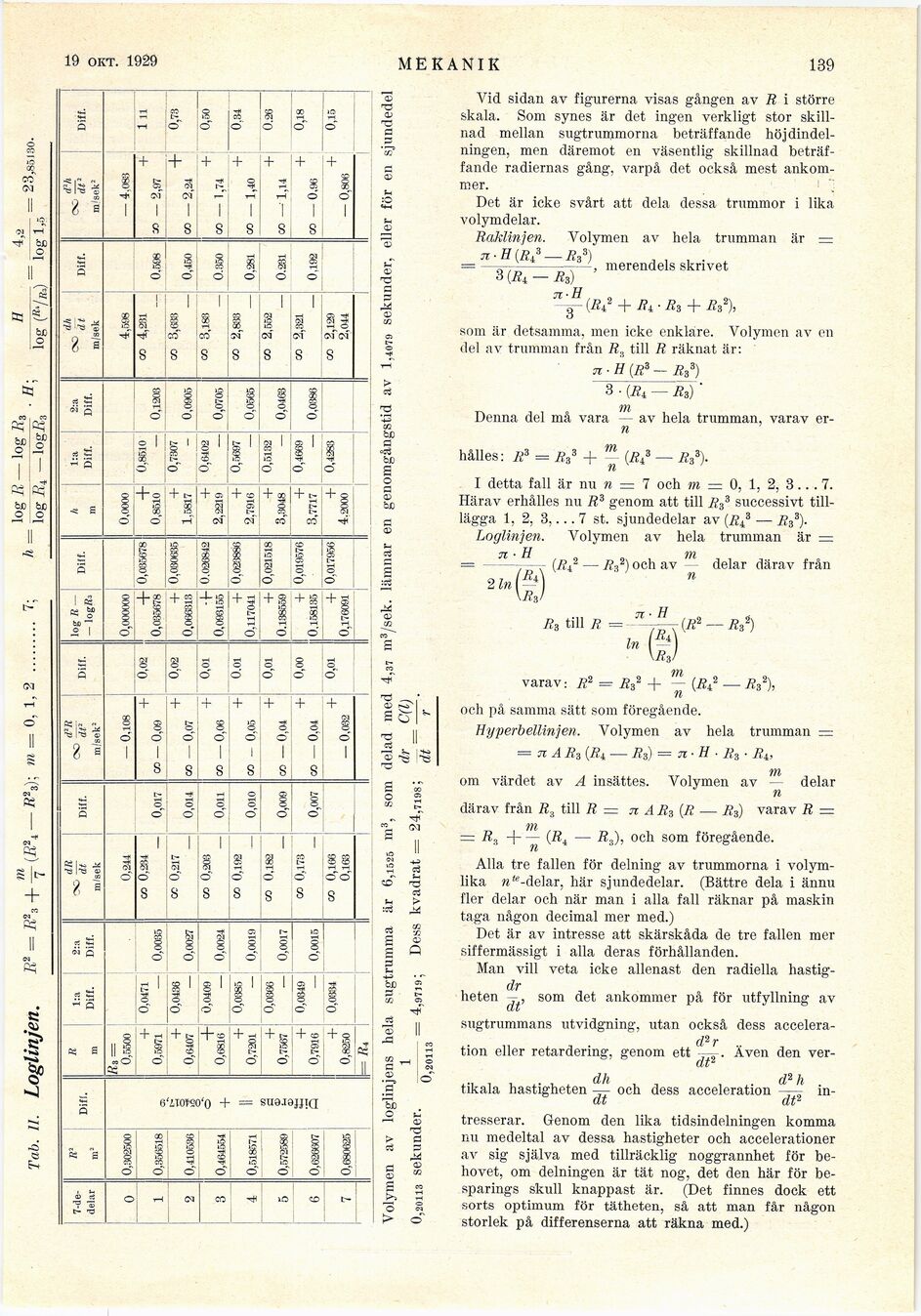
Tab. u. Loglinjen.
17)
tf = tf3 + — (E24 — B23); m = 0, 1, 2 ......... 7;
, logli — \ogK3 H 4,2
h = –T–r– • tf; .– = -— . = 23,85130.
log rj — logi?3 log (r’/r>) tog _
[-7-de-delar-]
{+7-de- delar+} B’ ma Diff. « l:a m 1 Diff. dR Diff. °° * m/sek d’R 00 dF m/sek2 Diff. log R
-— logßä Diff. h m l:a Diff. 2:a Diff. dh 00 dt Diff. m/sek d’H 00 dt’ m/sek2 Diff.
Vid sidan av figurerna visas gången av R i större
skala. Som synes är det ingen verkligt stor
skillnad mellan sugtrummorna beträffande
höjdindel-ningen, men däremot en väsentlig skillnad
beträffande radiernas gång, varpå det också mest
ankommer. 1
Det är icke svårt att dela dessa trummor i lika
volymdelar.
RakUnjen. Volymen av hela trumman är =
= 71 -jt3—, merendels skrivet
3 (Ä4 - R3)
^(Ä*2 + Ri-R3 + R32),
som är detsamma, men icke enklare. Volymen av en
del av trumman från Ä3 till R räknat är:
n ■ H (R3 - Æ33)
3 ■ (Ä4 — R3) "
m
Denna del må vara — av hela trumman, varav
er-n
hålles: R3 = R33 + ™ (R3 — Ä33).
I detta fall är nu n — 7 och m = 0, 1, 2, 3... 7.
Härav erhålles nu R3 genom att till R33 successivt till-
lägga 1, 2, 3,... 7 st. sjundedelar av (R43 — R33).
Loglinjen. Volymen av hela trumman är =
71 • H 711
= - - (R,2— i?»2) och av delar därav från
-(I)
R3 till R = ■ 71 -(R2 — R^)
In (Ä4)
7YI
varav: R2 = R32 + — (Ä42 — R32),
och på samma sätt som föregående.
Hyperbellinien. Volymen av hela trumman =
= n A R3 (ä4 — R3) = 71 • H ■ R3 ■ ä4,
m
om värdet av A insättes. Volymen av — delar
därav från R3 till R = 71 A R3 (R — R3) varav R =
7yi
— Ra –(Ä4 — R3), och som föregående.
Alla tre fallen för delning av trummorna i
volymlika wfe-delar, här sjundedelar. (Bättre dela i ännu
fler delar och när man i alla fall räknar på maskin
taga någon decimal mer med.)
Det är av intresse att skärskåda de tre fallen mer
siffermässigt i alla deras förhållanden.
Man vill veta icke allenast den radiella
hastiger
heten —som det ankommer på för utfyllning av
sugtrummans utvidgning, utan också dess accelera-
d2 r
tion eller retardering, genom ett —„-. Även den ver-
dt1
dh d2 h
tikala hastigheten — och dess acceleration ——
in-dt dt2
tresserar. Genom den lika tidsindelningen komma
nu medeltal av dessa hastigheter och accelerationer
av sig själva med tillräcklig noggrannhet för
behovet, om delningen är tät nog, det den här för
besparings skull knappast är. (Det finnes dock ett
sorts optimum för tätheten, så att man får någon
storlek på differenserna att räkna med.)
ßa =
0 0,302500 0,5500 0,244 — 0,108_____O^OOOOOO__________|_O0000 ___4,598 — 4,083
+ 0,0471 r co 0,234 + 0,02 + 0,035678 -f 0,8510 CO 4,231 + ; 111
1 0,356518 o, 0,6971 —| 0,0035 _— 0,017 CO — 0,09 _ 0,035678 ____0,8510......~ 0,1206 ______— 0,598 » — 2,97__I
g + 0,0436 ! .....CO 0,217 + 0,02 + 0,030635 + 0,7307 co 3,633 + 0,73
2 0,410536 I 0,6407 ’ —i 0,0027 — 0,014 co — 0,07 ___ 0.0663J3____1,5817 - 0,0905 : _0,450 CO — 2,24 ______
i-— o- X 0,0409 I co 0,203 + 0,01 -f- 0,026842 + 0,6402 co 3,183 + 0,50
3 0,464554 . 0,6816 — 0,0024 — 0,011 CO — 0,06 [ 0,093155 _____2,2219 J_— 0,0705____— 0.350 CO—1,74___
~ 0,0385 T CO 0,192 + 0,01 I + 0,023886 + 0,5697 CO 2,833 + 0,34
4 0,518571 « 0,7201 — 0,0019 _— 0,010 CO - 0,05__0,117011__2,7916 _j— 0,0565 __— _0,281_ CO — 1,40________________
g ~T~Ö,0366~ CO 0,182 + 0,01 -f- 0,021518 + 0,5132 CO 2,552 + 0.26
5 0,572589 2 0,7567 — 0,0017 — 0,009 CO —0,04 0.136559 3,30tö___— 0,0463___— 0.381 00 —1,14__________
H ......T "070349 CO 0,173 " "+ 0,00 +0,019578 ~ + 0,4669 CO 2,321 + 0,18
6 0,626607! Q 0,7916 — 0,0015_ _— _ 0,007 co —0,04 10.168185 •___3,7717____— 0,0386 ___— 0,192 CO — 0,96__
""’+ 0 0334 co 0,166 + 0,01 + 0,017956 + 0,4283 CO 2,129 + 0,15
7 0,680625 I 0,8250 0,163 __— 0,032 0,176091 ____4,2000 ______2,044 — 0,806_______
1 I fä" \ ~ r_. _______r__
Volymen av loglinjens hela sugtrumma är 6,1525 m3, som delad med 4,37 m3/sek. lämnar en genomgångstid av 1,4079 sekunder, eller för en sjundedel
1 dr C(l)
0,20113 sekunder. –––––= 4,9719; Dess kvadrat = 24,7198; ,; = —-•
0,20113 al ’
<< prev. page << föreg. sida << >> nästa sida >> next page >>