
Full resolution (TIFF) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
30
TEKNISK
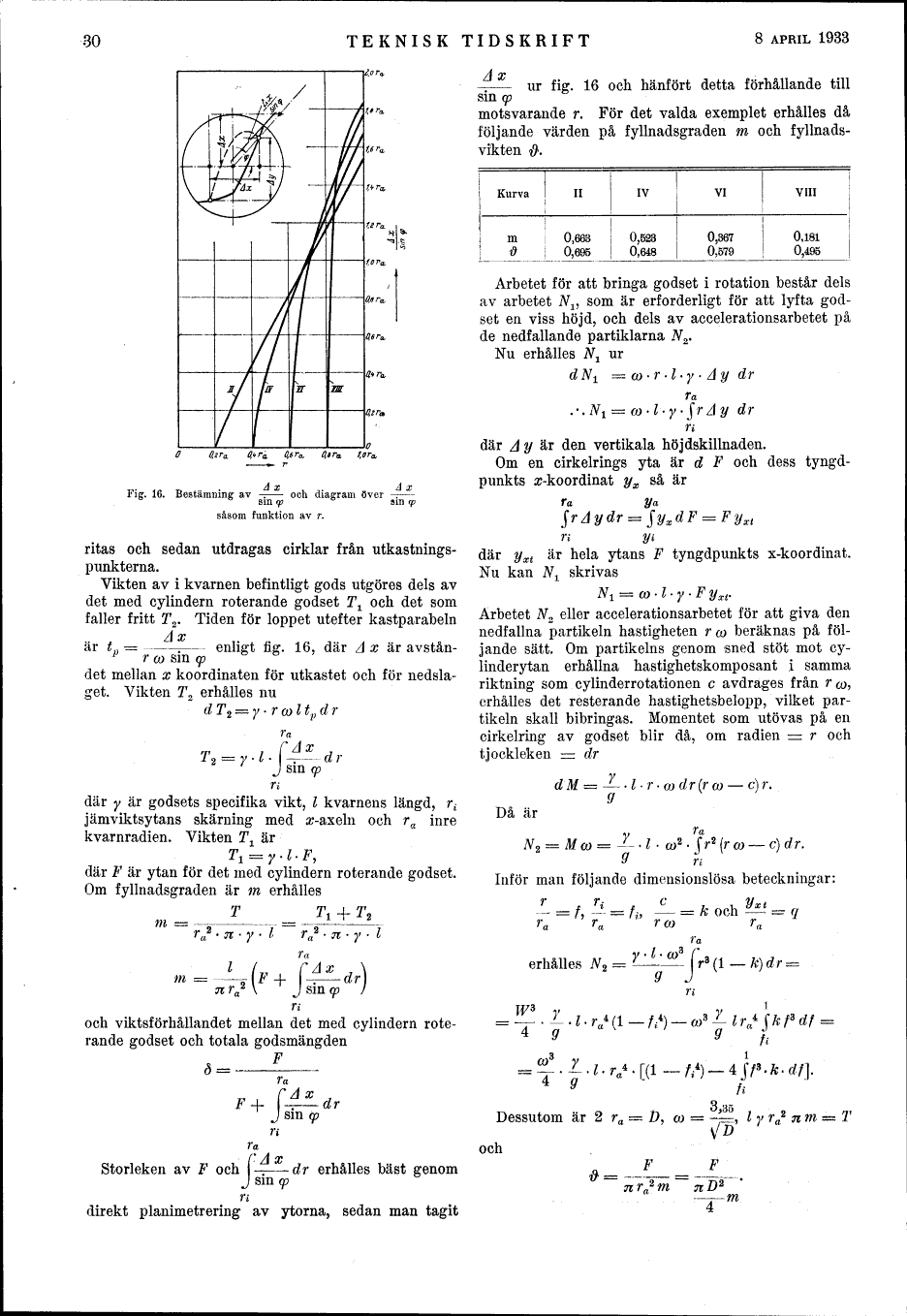
Fig. 16. Bestämning av - - och diagram över .
sin <p sm fp
såsom funktion av r.
ritas och sedan utdragas cirklar från
utkastnings-punkterna.
Vikten av i kvarnen befintligt gods utgöres dels av
det med cylindern roterande godset T± och det som
faller fritt T2. Tiden för loppet utefter kastparabeln
A fY»
är t - –––- : ––- enligt fig. 16. där A x är avstån-
1 r a) sm cp
det mellan x koordinaten för utkastet och för
nedslaget. Vikten T2 erhålles nu
d T 2 =
r coltpdr
d r
J sm (p
n
där y är godsets specifika vikt, l kvarnens längd, r{
jämviktsytans skärning med ar-axeln och ra inre
kvarnradien. Vikten 771 är
där F är ytan för det ined cylindern roterande godset.
Om fyllnadsgraden är m erhålles
T T! + T2
m =
ra2 - n . y - l
ra
1’a
- n -
m ==
nra
sm
och viktsförhållandet mellan det med cylindern
roterande godset och totala godsmängden
F+
1 sin (p
Ta
Storleken av F och
sn
-dr erhålles bäst genom
direkt planimetrering av ytorna, sedan man tagit
-?_ ur fig. 16 och hänfört detta förhållande till
sm (p
motsvarande r. För det valda exemplet erhålles då
följande värden på fyllnadsgraden m och
fyllnads-vikten $.
j
Kurva II IV VI VIII i
l !
___________________i________________________________________________________________i_________________________j
i m j 0,663 0,523 0,367 ! 0,181
j <d j 0,695 0,648_________0,579___________0,495
Arbetet för att bringa godset i rotation består dels
av arbetet N1? som är erforderligt för att lyfta
godset en viss höjd, och dels av accelerationsarbetet på
de nedfallande partiklarna N2.
Nu erhålles N^ ur
dN± = co-r -l-y > Ay dr
Ta
...Ni = co -1-y- §rA y dr
n
där A y är den vertikala höjdskillnaden.
Om en cirkelrings yta sn d F och dess
tyngdpunkts z-koordinat yx så är
n yi
där yxt är hela ytans F tyngdpunkts x-koordinat.
Nu kan N± skrivas
Nl = a)’l’7-F yxt.
Arbetet N2 eller accelerationsarbetet för att giva den
nedfallna partikeln hastigheten r co beräknas på
följande sätt. Om partikelns genom sned stöt mot
cylinderytan erhållna hastighetskomposant i samma
riktning som cylinderrotationen c avdrages från r co,
erhålles det resterande hastighetsbelopp, vilket
partikeln skall bibringas. Momentet som utövas på en
cirkelring av godset blir då, om radien = r och
tjockleken - dr
d M =
Då är
j
- r - a)dr(r co - c)r.
N2 = M co == - . l - co2 . Jr2 (r co - c) dr.
^ n
Inför man följande dimensionslösa beteckningar:
.L - f 1± - f __ k
ra~r’ra-h> ra>~K
Ta
’ . l - CO3 (\
erhålles ]V2
fi
Dessutom är 2 ra = Ö, co =
och
F
-,
\/D
F
nV* ’
. .. m
ra2 n m = T
<< prev. page << föreg. sida << >> nästa sida >> next page >>