
Full resolution (TIFF) - On this page / på denna sida - Häfte 11. Nov. 1934 - Torsten Henning: Elektrisk beräkning av distributionsnät
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
3 NOV. 1934
ELEKTROTEKNIK
163
kontinuerlig överblick över spänningsfallets och
förlusternas variation med area och effektfaktor, vilket
senare är särskilt önskvärt vid projektering av en
kraftöverföring.
Det må påpekas, att man vid
spänningsfallsberäk-ning med linjaldiagrammet ej nödvändigtvis först
behöver beräkna kilometervärdet, ty utgår man från
W W
– . l i stället för - , erhålles direkt spänningsfallet
L/ L
tör hela sträckan 1. Vill man i detta sammanhang
samtidigt avläsa förlusterna, måste man komma
ihåg, att det då å skala 4 avlästa talet har
dimensionen kW . km och alltså måste divideras med
linje-längden för att linjesträckans effektförlust skall
erhållas. Vid beräkningar å redan förefintliga nät
torde det dock vara lämpligast att genomgående
räkna med km-värden, enär man för att avgöra
ekonomien vid en eventuell lin j ef or stärkning ändock
måste hava kännedom om effektförlustens värde
pr km.
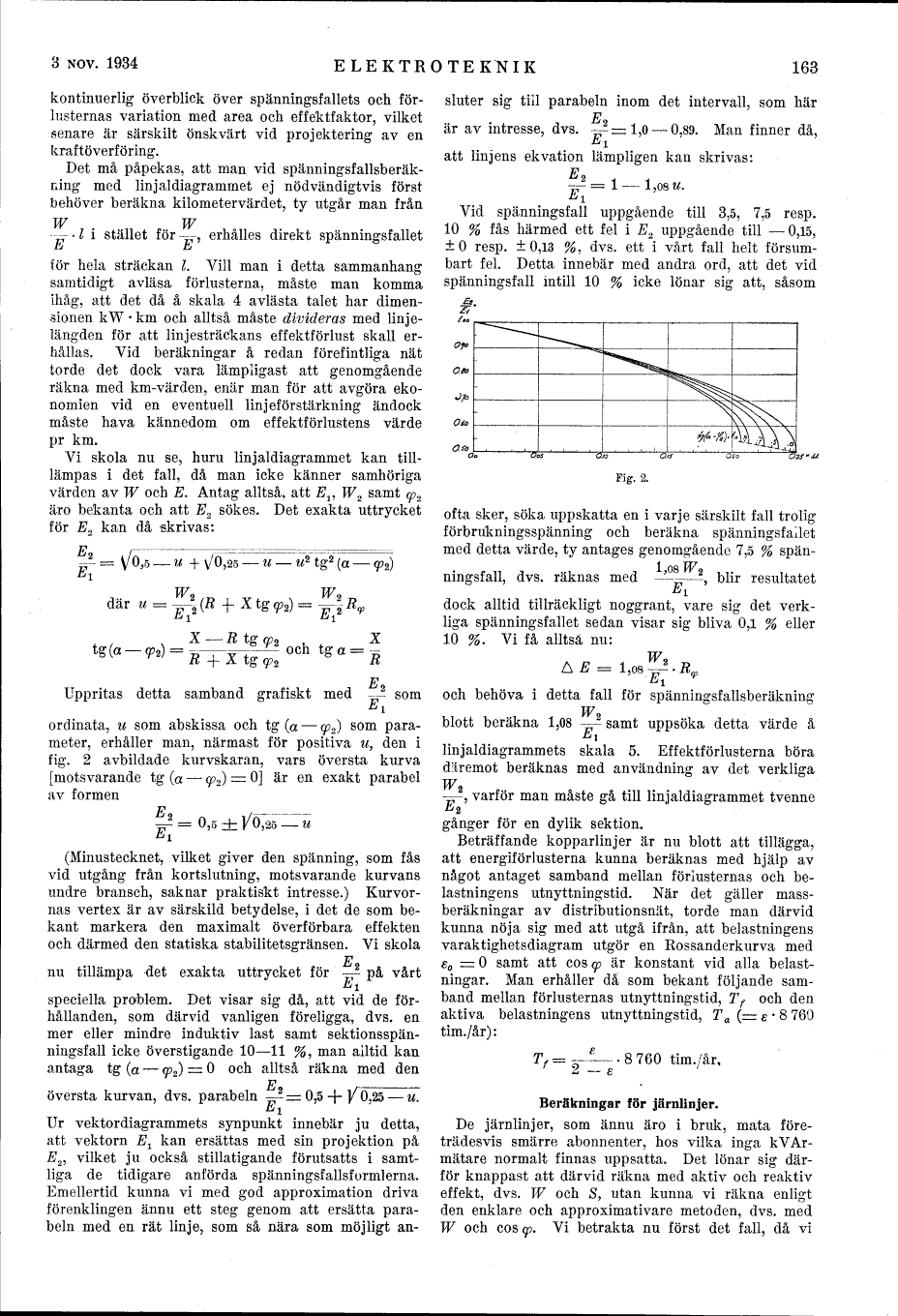
Vi skola nu se, huru linjaldiagrammet kan
till-lämpas i det fall, då man icke känner samhöriga
värden av W och E. Antag alltså, att E^ W2 samt <^2
äro bekanta och att E2 sökes. Det exakta uttrycket
för E2 kan då skrivas:
-A = V/0,5
där M =
f1
Uppritas detta samband grafiskt med -? som
Ei
ordinata, u som abskissa och tg (a - <p2) som
parameter, erhåller man, närmast för positiva u, den i
fig. 2 avbildade kurvskaran, vars översta kurva
[motsvarande tg (a - cp2) = 0] är en exakt parabel
av formen
-J = 0,5 ± /0,25
(Minustecknet, vilket giver den spänning, som fås
vid utgång från kortslutning, motsvarande kurvans
undre bransch, saknar praktiskt intresse.)
Kurvornas vertex är av särskild betydelse, i det de som
bekant markera den maximalt överförbara effekten
och därmed den statiska stabilitetsgränsen. Vi skola
p<
nu tillämpa det exakta uttrycket för – på vårt
speciella problem. Det visar sig då, att vid de
förhållanden, som därvid vanligen föreligga, dvs. en
mer eller mindre induktiv last samt
sektionsspänningsfall icke överstigande 10 - 11 %, man alltid kan
antaga tg (a - <^2) - O och alltså räkna med den
.p _
översta kurvan, dvs. parabeln ~ - 0,;5 + ]/ 0,25 - u.
Ll
Ur vektordiagrammets synpunkt innebär ju detta,
att vektorn E1 kan ersättas med sin projektion på
#25 vilket ju också stillatigande förutsatts i
samtliga de tidigare anförda spänningsfallsformlerna.
Emellertid kunna vi med god approximation driva
förenklingen ännu ett steg genom att ersätta
parabeln med en rät linje, som så nära som möjligt an-
sluter sig till parabeln inom det intervall, som här
rr
är av intresse, dvs. -^-1,0-0,89. Man finner då,
1
att linjens ekvation lämpligen kan skrivas:
- = l –– 1,08 U.
Vid spänningsfall uppgående till 3,5, 7,5 resp.
10 % fås härmed ett fel i E2 uppgående till –0,15,
±0 resp. ±0,13 %, dvs. ett i vårt fall helt
försumbart fel. Detta innebär med andra ord, att det vid
spänningsfall intill 10 % icke lönar sig att, såsom
Fig. 2.
ofta sker, söka uppskatta en i varje särskilt fall trolig
förbrukningsspänning och beräkna spänningsfallet
med detta värde, ty antages genomgående 7,5 %
spänningsfall, dvs. räknas med ––––, blir resultatet
EI
dock alltid tillräckligt noggrant, vare sig det
verkliga spänningsfallet sedan visar sig bliva 0,1 % eller
10 %. Vi få alltså nu:
W
A E= 1,08 ’B
bl
och behöva i detta fall för spänningsfallsberäkning
W»
blott beräkna 1,08 – samt uppsöka detta värde å
^i
linjaldiagrammets skala 5. Effektförlusterna böra
däremot beräknas med användning av det verkliga
W*
-, varför man måste gå till linjaldiagrammet tvenne
L2
gånger för en dylik sektion.
Beträffande kopparlinjer är nu blott att tillägga,
att energiförlusterna kunna beräknas med hjälp av
något antaget samband mellan förlusternas och
belastningens utnyttningstid. När det gäller
massberäkningar av distributionsnät, torde man därvid
kunna nöja sig med att utgå ifrån, att belastningens
varaktighetsdiagram utgör en Rossanderkurva med
s0 = O samt att cos cp är konstant vid alla
belastningar. Man erhåller dä som bekant följande
samband mellan förlusternas utnyttningstid, Tf och den
aktiva belastningens utnyttningstid, Ta (== s . 8 760
tim./år):
Tf = ^- - 8 760 tim./år,
E
Beräkningar för järnlinjer.
De järnlinjer, som ännu äro i bruk, mata
företrädesvis smärre abonnenter, hos vilka inga kV
Ar-mätare normalt finnas uppsatta. Det lönar sig
därför knappast att därvid räkna med aktiv och reaktiv
effekt, dvs. W och S, utan kunna vi räkna enligt
den enklare och approximativare metoden, dvs. med
W och cos q). Vi betrakta nu först det fall, då vi
<< prev. page << föreg. sida << >> nästa sida >> next page >>