
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskri i t
1.00
Va
QSO
Q40
Qso
åisre kurvan £0
nec/re –– EOO
GO äO
eoo X_ ooo
a
1 W. Toixmien : Berechnung Turbulenter
Ausbreitungsvor-gänge. Zeitschr. f. angew. Math. u. Al och. 1926, s 469.
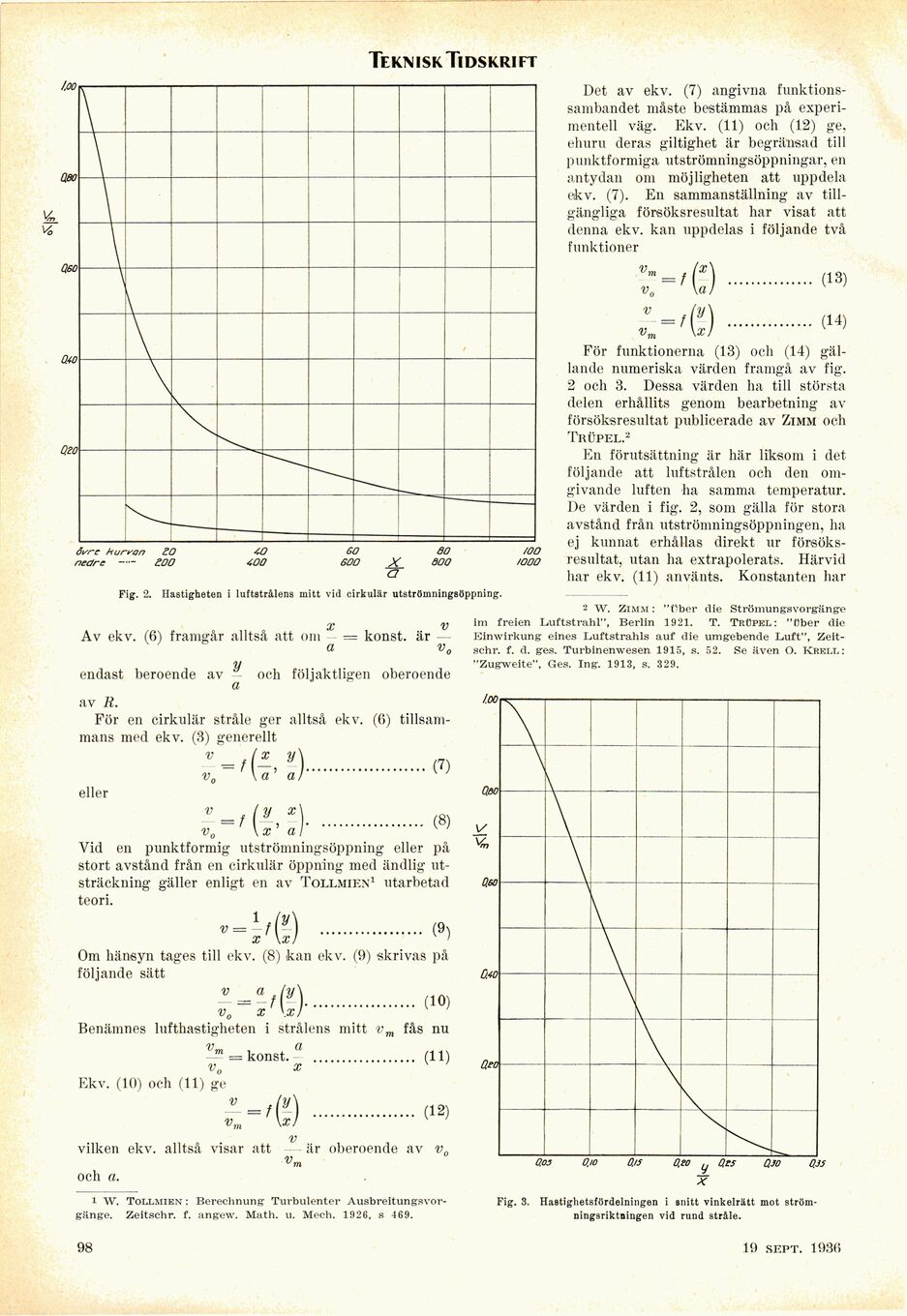
Fig. 3. Hastighetsfördelningen i snitt vinkelrätt mot
ström-ningsriktningen vid rund stråle.
98
19 sept. 1936
Det- av ekv. (7) angivna
funktionssambandet måste bestämmas på
experimentell väg. Ekv. (11) och (12) ge,
ehuru deras giltighet är begränsad till
punktformiga utströmningsöppningar, en
antydan om möjligheten att uppdela
ekv. (7). En sammanställning av
tillgängliga försöksresultat har visat att
denna ekv. kan uppdelas i följande två
funktioner
m = †[ ............... (13)
v0 \al
...............<">
För funktionerna (13) och (14)
gällande numeriska värden framgå av fig.
2 och 3. Dessa värden ha till största
delen erhållits genom bearbetning av
försöksresultat publicerade av Zimm och
Trüpel.2
En förutsättning är här liksom i det
följande att luftstrålen och den
omgivande luften ha samma temperatur.
De värden i fig. 2, som gälla för stora
avstånd från utströmningsöppningen, ha
ej kunnat erhållas direkt ur
försöksresultat, utan ha extrapolerats. Härvid
har ekv. (11) använts. Konstanten har
Fig. 2. Hastigheten i luftstrålens mitt vid cirkulär utströmningsöppning.
X V
Av ekv. (6) framgår alltså att om = konst, är
a v0
v
endast beroende av - och följaktligen oberoende
a
av R.
För en cirkulär stråle ger alltså ekv. (6)
tillsammans med ekv. (3) generellt
v l x y\
= M-> .....................(7
v0 \ a al
eller
................... (8)
v0 \x al
Vid en punktformig utströmningsöppning eller på
stort avstånd från en cirkulär öppning med ändlig
utsträckning gäller enligt en av Tollmien1 utarbetad
teori.
..................<9>
Om hänsyn tages till ekv. (8) kan ekv. (9) skrivas på
följande sätt
v a /y\
- = ...................(10)
V0 X \x)
Benämnes lufthastigheten i strålens mitt vm fås nu
konst.0 .................. (11)
V X
Ekv. (10) och (11) ge
..................<12>
v
vilken ekv. alltså visar att — är oberoende av v0
Vm
och a.
W. Zimm : "Ober die Strömungsvorgänge
im freien Luftstrahl", Berlin 1921. T. Trüpel: "Ober die
Einwirkung eines Luftstrahls auf die umgebende Luft",
Zeitschr. f. d. ges. Turbinenwesen 1915, s. 52. Se även O. Krktx :
"Zugweite", Ges. Ing. 1913, s. 329.
<< prev. page << föreg. sida << >> nästa sida >> next page >>