
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Mekanik
terade för det omfattande arbete, som av dem nedlagts
på frågans behandling. Vidare framfördes ett tack till
de firmor och institutioner, som bidragit till
undersökningarnas genomförande. Bn.
INSÄNT
Ekonomisk verkningsgrad.
Med största tacksamhet och intresse har säkert
många med mig tagit del av civilingenjör Genbergs
artikel om "Ekonomisk verkningsgrad", som fanns införd
i Mekaniks majhäfte i år. Den problemställning, som
ingenjör Genberg gjort i sin framställning, är just den
som osökt måste göras, då man sysslar med
tidsstudiearbete under förhållanden, där en arbetare har att sköta
flera maskiner. Problemet synes nu vara moget att
upptagas till allmän behandling, då det uppställts och
bearbetats på flera håll, med olika utgångspunkter. Även
författaren till detta inlägg har sedan fem år tillbaka
sysslat med sådana undersökningar och härunder
använt en något avvikande lösning av problemet, som dock
visat sig fylla alla berättigade anspråk på tillförlitlighet.
Jag hoppas att i ett följande nummer av tidskriften fä
framlägga denna lösning och vill nu endast något
granska ingenjör Genbergs behandling av problemet. En
diskussion av detta, för särskilt textilindustrien så
viktiga problem, torde vara av största intresse.
a) Maskintidsperioderna, enl. föregående
framställning, komma givetvis att ha olika längd. De allra
kortaste uppträda relativt sällan liksom de allra längsta. De
flesta hålla sig i närheten av de medellånga perioderna.
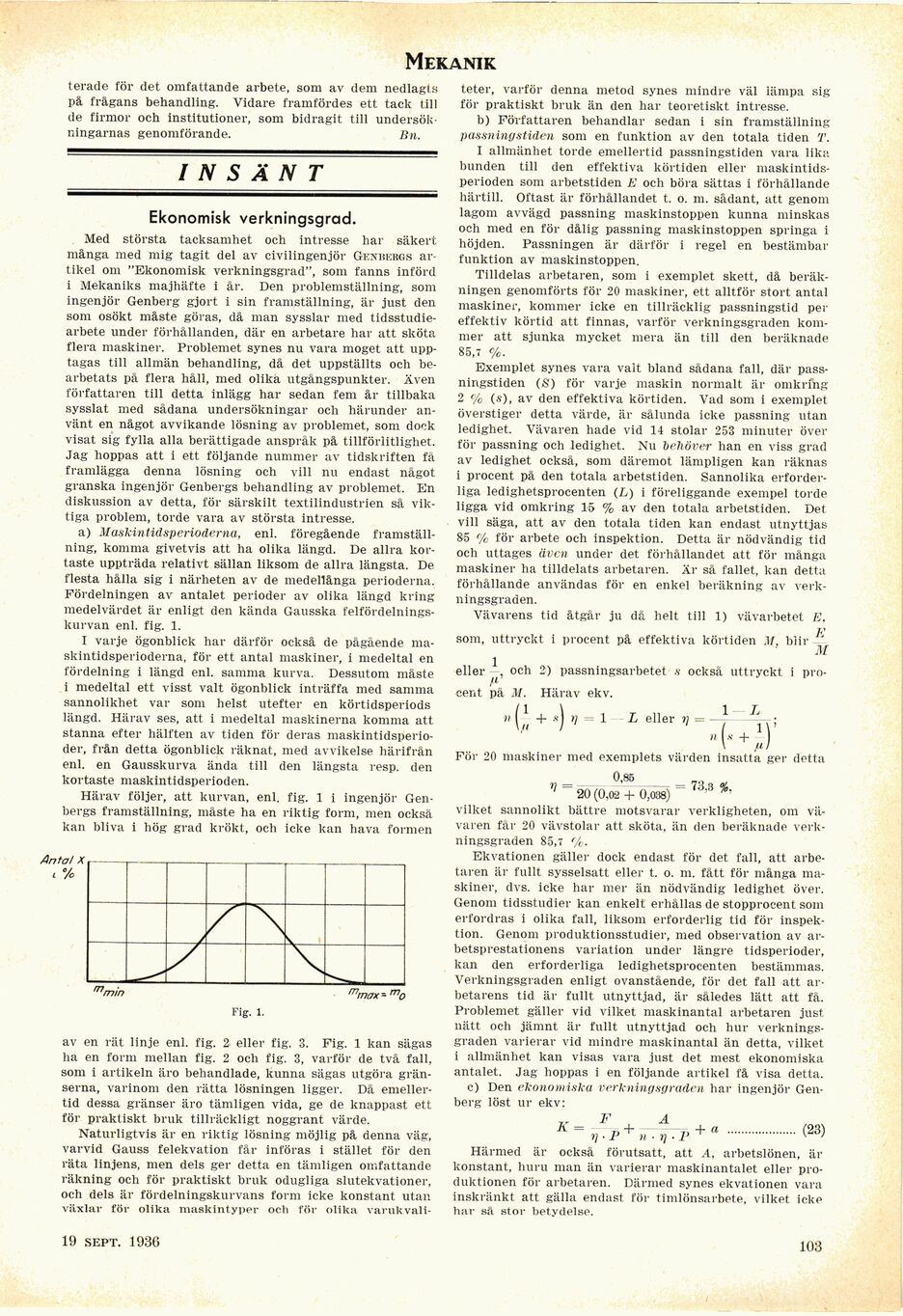
Fördelningen av antalet perioder av olika längd kring
medelvärdet är enligt den kända Gausska
felfördelnings-kurvan enl. fig. 1.
I varje ögonblick har därför också de pågående
maskintidsperioderna, för ett antal maskiner, i medeltal en
fördelning i längd enl. samma kurva. Dessutom måste
i medeltal ett visst valt ögonblick inträffa med samma
sannolikhet var som helst utefter en körtidsperiods
längd. Härav ses, att i medeltal maskinerna komma att
stanna efter hälften av tiden för deras
maskintidsperioder, från detta ögonblick räknat, med avvikelse härifrån
enl. en Gausskurva ända till den längsta resp. den
kortaste maskintidsperioden.
Härav följer, att kurvan, enl. fig. 1 i ingenjör
Genbergs framställning, måste ha en riktig form, men också
kan bliva i hög grad krökt, och icke kan hava formen
Antal X
< %
teter, varför denna metod synes mindre väl iämpa sig
för praktiskt bruk än den liar teoretiskt intresse.
b) Författaren behandlar sedan i sin framställning
passningstiden som en funktion av den totala tiden T.
I allmänhet torde emellertid passningstiden vara lika
bunden till den effektiva körtiden eller
maskintidsperioden som arbetstiden E och böra sättas i förhållande
härtill. Oftast är förhållandet t. o. m. sådant, att genom
lagom avvägd passning maskinstoppen kunna minskas
och med en för dålig passning maskinstoppen springa i
höjden. Passningen är därför i regel en bestämbar
funktion av maskinstoppen.
Tilldelas arbetaren, som i exemplet skett, då
beräkningen genomförts för 20 maskiner, ett alltför stort antal
maskiner, kommer icke en tillräcklig passningstid per
effektiv körtid att finnas, varför verkningsgraden
kommer att sjunka mycket mera än till den beräknade
85,7 %.
Exemplet synes vara valt bland sådana fall, där
passningstiden (S) för varje maskin normalt är omkring
2 c/0 (s), av den effektiva körtiden. Vad som i exemplet
överstiger detta värde, är sålunda icke passning utan
ledighet. Vävaren hade vid 14 stolar 253 minuter över
för passning och ledighet. Nu behöver han en viss grad
av ledighet också, som däremot lämpligen kan räknas
i procent på den totala arbetstiden. Sannolika
erforderliga ledighetsprocenten (L) i föreliggande exempel torde
ligga vid omkring 15 % av den totala arbetstiden. Det
vill säga, att av den totala tiden kan endast utnyttjas
85 % för arbete och inspektion. Detta är nödvändig tid
och uttages även under det förhållandet att för många
maskiner ha tilldelats arbetaren. Är så fallet, kan detta
förhållande användas för en enkel beräkning av
verkningsgraden.
Vävarens tid åtgår ju då helt till 1) vävarbetet E,
E
som, uttryckt i procent
effektiva körtiden .V. blir
M
Fig. l.
av en rät linje enl. fig. 2 eller fig. 3. Fig. 1 kan sägas
ha en form mellan fig. 2 och fig. 3, varför de två fall,
som i artikeln äro behandlade, kunna sägas utgöra
gränserna, varinom den rätta lösningen ligger. Då
emellertid dessa gränser äro tämligen vida, ge de knappast ett
för praktiskt bruk tillräckligt noggrant värde.
Naturligtvis är en riktig lösning möjlig på denna väg,
varvid Gauss felekvation får införas i stället för den
räta linjens, men dels ger detta en tämligen omfattande
räkning och för praktiskt bruk odugliga slutekvationer,
och dels är fördelningskurvans form icke konstant utan
växlar för olika maskintyper och för olika varukvali-
eller , och 2) passningsarbetet .v också uttryckt i
pro-fl
cent på M. Härav ekv.
" 11 + *) n = 1 L eller V = " T TV
’T + J
För 20 maskiner med exemplets värden insatta ger detta
0,85
V ~ 20 (0,02 + 0,038) ~ ’3
vilket sannolikt bättre motsvarar verkligheten, om
vävaren får 20 vävstolar att sköta, än den beräknade
verkningsgraden 85,7 c/c.
Ekvationen gäller dock endast för det fall, att
arbetaren är fullt sysselsatt eller t. o. m. fått för många
maskiner, dvs. icke har mer än nödvändig ledighet över.
Genom tidsstudier kan enkelt erhållas de stopprocent som
erfordras i olika fall, liksom erforderlig tid för
inspektion. Genom produktionsstudier, med observation av
arbetsprestationens variation under längre tidsperioder,
kan den erforderliga ledighetsprocenten bestämmas.
Verkningsgraden enligt ovanstående, för det fall att
arbetarens tid är fullt utnyttjad, är således lätt att få.
Problemet gäller vid vilket maskinantal arbetaren just
nätt och jämnt är fullt utnyttjad och hur
verkningsgraden varierar vid mindre maskinantal än detta, vilket
i allmänhet kan visas vara just det mest ekonomiska
antalet. Jag hoppas i en följande artikel få visa detta.
c) Den ekonomiska verkningsgraden har ingenjör
Genberg löst ur ekv:
A t. + ° .................... (23)
_ F
i] ■ 1’ + n■ i] ■ 1’
Härmed är också förutsatt, att A, arbetslönen, är
konstant, huru man än varierar maskinantalet eller
produktionen för arbetaren. Därmed synes ekvationen vara
inskränkt att gälla endast för timlönsarbete, vilket icke
har så stor betydelse.
19 sept. 193g
103
<< prev. page << föreg. sida << >> nästa sida >> next page >>