
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
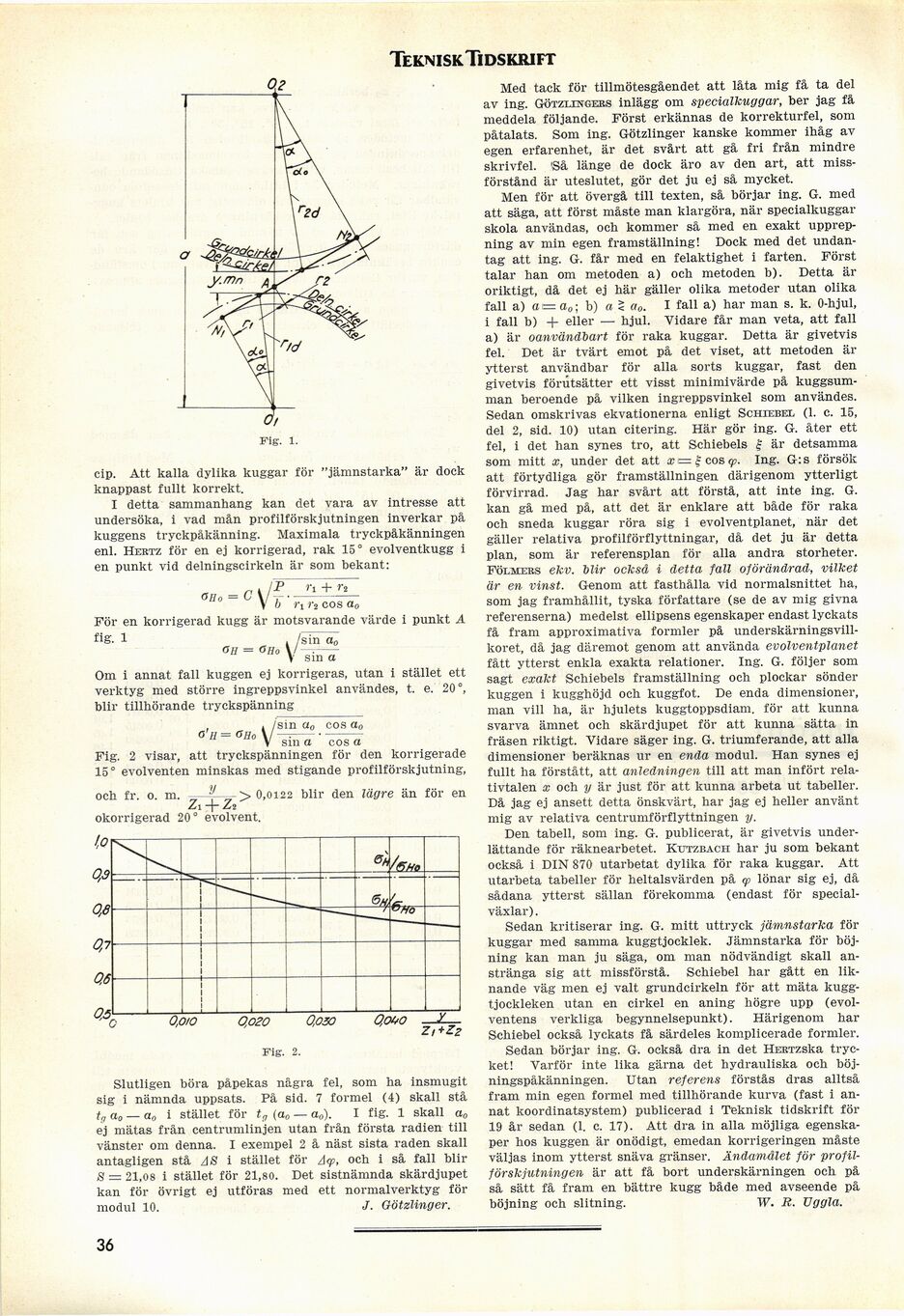
cip. Att kalla dylika kuggar för "jämnstarka" är dock
knappast fullt korrekt.
I detta sammanhang kan det vara av intresse att
undersöka, i vad mån profilförskjutningen inverkar på
kuggens tryckpåkänning. Maximala tryckpåkänningen
enl. Hertz för en ej korrigerad, rak 15° evolventkugg i
en punkt vid delningscirkeln är som bekant:
Oflo ■
Ti + r2
’ b Ti r2 eos a0
För en korrigerad kugg är motsvarande värde i punkt A
fiS- 1 . /Sn ä0
ag
OHo \i~
V sm a
Om i annat fall kuggen ej korrigeras, utan i stället ett
verktyg med större ingreppsvinkel användes, t. e. 20°,
blir tillhörande tryckspänning
O’H=oho y’
sm a„ eos a0
sin a
eos a
Fig. 2 visar, att tryckspänningen för den korrigerade
15° evolventen minskas med stigande profilförskjutning,
och fr. o. m. ’{ ->0,oi22 blir den lägre än för en
Zi -†- Zi
okorrigerad 20° evolvent.
lo
Fig. 2.
Slutligen böra påpekas några fel, som ha insmugit
sig i nämnda uppsats. På sid. 7 formel (4) skall stå
tg a„ — a o i stället för tg (a0 — a0). I fig. 1 skall a0
ej mätas från centrumlinjen utan från första radien till
vänster om denna. I exempel 2 å näst sista raden skall
antagligen stå zl<S i stället för A<p, och i så fall blir
8 — 21,08 i stället för 21,80. Det sistnämnda skärdjupet
kan för övrigt ej utföras med ett normalverktyg för
modul 10. J. Götzlinger.
Med tack för tillmötesgåendet att låta mig få ta del
av ing. Götzlingers inlägg om specialkuggar, ber jag få
meddela följande. Först erkännas de korrekturfel, som
påtalats. Som ing. Götzlinger kanske kommer ihåg av
egen erfarenhet, är det svårt att gå fri från mindre
skrivfel. Så länge de dock äro av den art, att
missförstånd är uteslutet, gör det ju ej så mycket.
Men för att övergå till texten, så börjar ing. G. med
att säga, att först måste man klargöra, när specialkuggar
skola användas, och kommer så med en exakt
upprepning av min egen framställning! Dock med det
undantag att ing. G. får med en felaktighet i farten. Först
talar han om metoden a) och metoden b). Detta är
oriktigt, då det ej här gäller olika metoder utan olika
fall a) a t= a0; b) a < a0. I fall a) har man s. k. 0-hjul,
i fall b) + eller — hjul. Vidare får man veta, att fall
a) är oanvändbart för raka kuggar. Detta är givetvis
fel. Det är tvärt emot på det viset, att metoden är
ytterst användbar för alla sorts kuggar, fast den
givetvis förutsätter ett visst minimivärde på
kuggsum-man beroende på vilken ingreppsvinkel som användes.
Sedan omskrivas ekvationerna enligt Schiebel (1. c. 15,
del 2, sid. 10) utan citering. Här gör ing. G. åter ett
fel, i det han synes tro, att Schiebels f är detsamma
som mitt x, under det att x<= |eoscp. Ing. G:s försök
att förtydliga gör framställningen därigenom ytterligt
förvirrad. Jag har svårt att förstå, att inte ing. G.
kan gå med på, att det är enklare att både för raka
och sneda kuggar röra sig i evolventplanet, när det
gäller relativa profilförflyttningar, då det ju är detta
plan, som är referensplan för alla andra storheter.
Fölmers ekv. blir också i detta fall oförändrad, vilket
är en vinst. Genom att fasthålla vid normalsnittet ha,
som jag framhållit, tyska författare (se de av mig givna
referenserna) medelst ellipsens egenskaper endast lyckats
få fram approximativa formler på
underskärningsvill-koret, då jag däremot genom att använda evolventplanet
fått ytterst enkla exakta relationer. Ing. G. följer som
sagt exakt Schiebels framställning och plockar sönder
kuggen i kugghöjd och kuggfot. De enda dimensioner,
man vill ha, är hjulets kuggtoppsdiam. för att kunna
svarva ämnet och skärdjupet för att kunna sätta in
fräsen riktigt. Vidare säger ing. G. triumferande, att alla
dimensioner beräknas ur en enda modul. Han synes ej
fullt ha förstått, att anledningen till att man infört
relativtalen x och y är just för att kunna arbeta ut tabeller.
Då jag ej ansett detta önskvärt, har jag ej heller använt
mig av relativa centrumförflyttningen y.
Den tabell, som ing. G. publicerat, är givetvis
underlättande för räknearbetet. Ktxtzbach har ju som bekant
också i DIN 870 utarbetat dylika för raka kuggar. Att
utarbeta tabeller för heltalsvärden på <p lönar sig ej, då
sådana ytterst sällan förekomma (endast för
specialväxlar).
Sedan kritiserar ing. G. mitt uttryck jämnstarka för
kuggar med samma kuggtjocklek. Jämnstarka för
böjning kan man ju säga, om man nödvändigt skall
anstränga sig att missförstå. Schiebel har gått en
liknande väg men ej valt grundcirkeln för att mäta
kugg-tjockleken utan en cirkel en aning högre upp
(evol-ventens verkliga begynnelsepunkt). Härigenom har
Schiebel också lyckats få särdeles komplicerade formler.
Sedan börjar ing. G. också dra in det HERTzska
trycket! Varför inte lika gärna det hydrauliska och
böj-ningspåkänningen. Utan referens förstås dras alltså
fram min egen formel med tillhörande kurva (fast i
annat koordinatsystem) publicerad i Teknisk tidskrift för
19 år sedan (1. c. 17). Att dra in alla möjliga
egenskaper hos kuggen är onödigt, emedan korrigeringen måste
väljas inom ytterst snäva gränser. Ändamålet för
profilförskjutningen är att få bort underskärningen och på
så sätt få fram en bättre kugg både med avseende på
böjning och slitning. W. R. Uggla.
36
<< prev. page << föreg. sida << >> nästa sida >> next page >>