
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Mekanik.
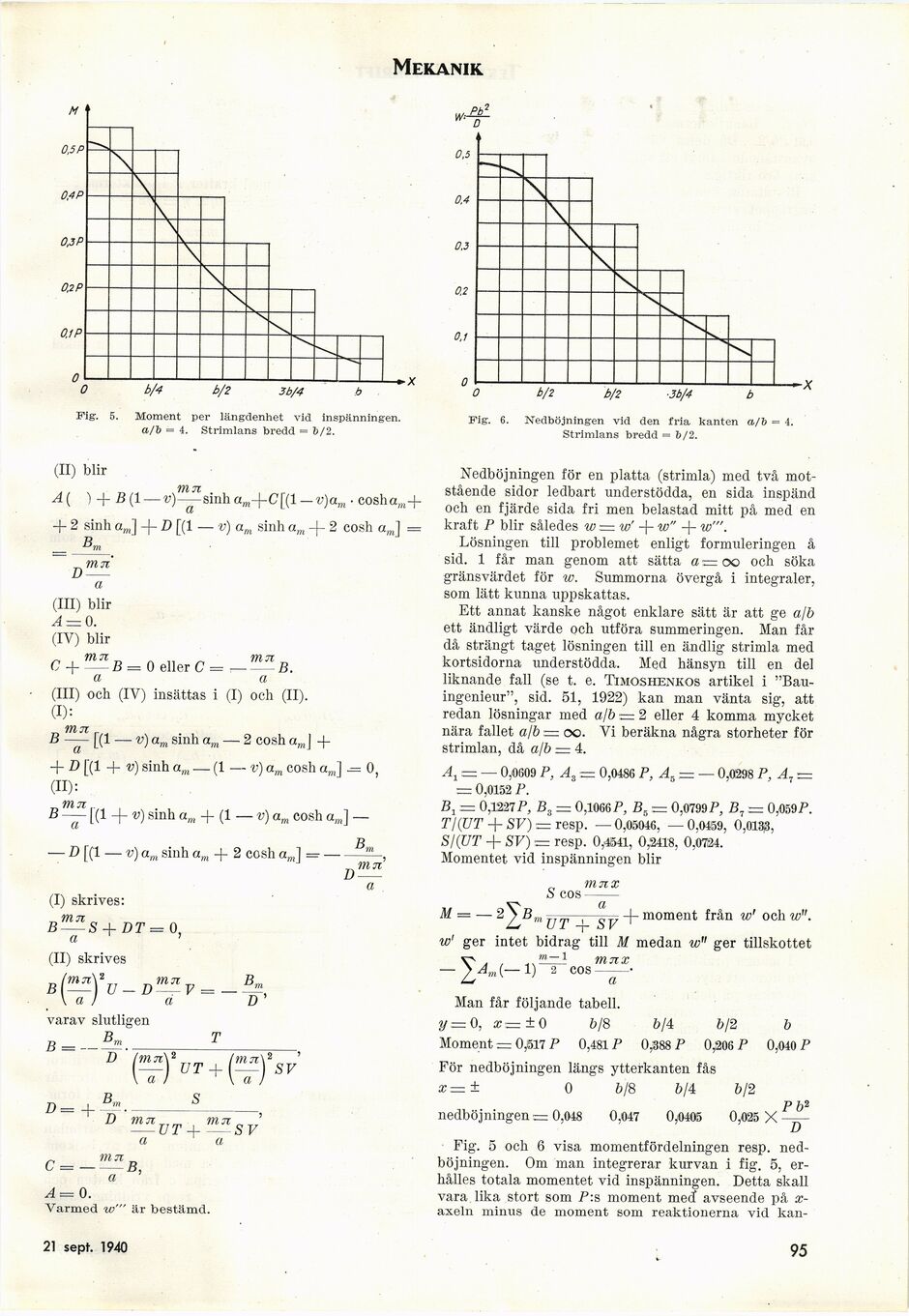
Fig. 5. Moment per längdenhet vid Inspänningen.
a./6 = 4. Strimlans bredd = 6/2.
Fig. 6. Nedböjningen vid den fria kanten a/6 = 4.
Strimlans bredd = 6/2.
(II) blir
mn
A( ) + B(l — v)-^-sinham+C[(l-v)am ■ cosh a,„+
+ 2 sinh a,„] -f D [(1 — v) am siiih am -(- 2 cosh am] =
Bm
mn
D
a
(III) blir
A — 0.
(IV) blir
C + ^B
a
0 eller C = -
myr
-J3.
(III) och (IY) insättas i (I) och (II).
(I):
m n
B —— [(1 — v) am sinh am — 2 cosh am\ -|-
+ D [(1 + v) sinh am — (1 — v) am cosh am] –- 0,
(II):
7YI 71
B — [(1 -f v) sinh am + (1 — v) am cosh am] —
B„,
— D [(1 — v) am sinh am -|- 2 cosh am]
(I) skrives:
B^S + DT^ 0,
a
D
mn
(II) skrives
B
U ■
BmnV =
ä
Bm
D ’
varav slutligen
Bm
B = —-
D= +
D
B,„
-UT A–-SV
a a
a
A= 0.
Varmed w’" är bestämd.
Nedböjningen för en platta (strimla) med två
motstående sidor ledbart understödda, en sida inspänd
och en fjärde sida fri men belastad mitt på med en
kraft P blir således w — w’ + w" + w’".
Lösningen till problemet enligt formuleringen å
sid. 1 får man genom att sätta a —oo och söka
gränsvärdet för w. Summorna övergå i integraler,
som lätt kunna uppskattas.
Ett annat kanske något enklare sätt är att ge a/b
ett ändligt värde och utföra summeringen. Man får
då strängt taget lösningen till en ändlig strimla med
kortsidorna understödda. Med hänsyn till en del
liknande fall (se t. e. Timoshenkos artikel i
"Bau-ingenieur", sid. 51, 1922) kan man vänta sig, att
redan lösningar med a/b ■— 2 eller 4 komma mycket
nära fallet alb = oo. Vi beräkna några storheter för
strimlan, då a/b = 4.
At — — 0,0609 P, A3 = 0,0486 P, A5 = — 0,0298 P, A7 —
= 0,0152 P.
B1 = 0,1227 P, B3 = 0.1066 P, B. = 0,0799 P, ß7 = 0,059
T/(UT + SF) = resp. —0,05046, —0,0459, 0,013£,
SI (UT + SF) = resp. 0,4541, 0,2418, 0,0724.
Momentet vid inspänningen blir
M
2IB>
mnx
S eos - —
a
- moment från w’ och w".
UT -f SV
w’ ger intet bidrag till M medan w" ger tillskottet
mnx
m— 1
• 1) 2 cos
a
bl 4
0,388 P
fe/2
0,206 P
b
0,040 P
Man får följande tabell.
y = 0, æ:=±0 fe/8
Moment = 0,i5l7 P 0,481 P
För nedböjningen längs ytterkanten fås
x=z± 0 fe/8 fe/4 fe/2
Pb2
nedböjningen = 0,048 0,047 0,0405 0,025 X —-
Fig. 5 och 6 visa momentfördelningen resp.
nedböjningen. Om man integrerar kurvan i fig. 5,
erhålles totala momentet vid inspänningen. Detta skall
vara lika stort som P:s moment med avseende på
x-axeln minus de moment som reaktionerna vid kan-
21 sept. 1940
95
<< prev. page << föreg. sida << >> nästa sida >> next page >>