
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
Sidosfämning
Sidosfämning
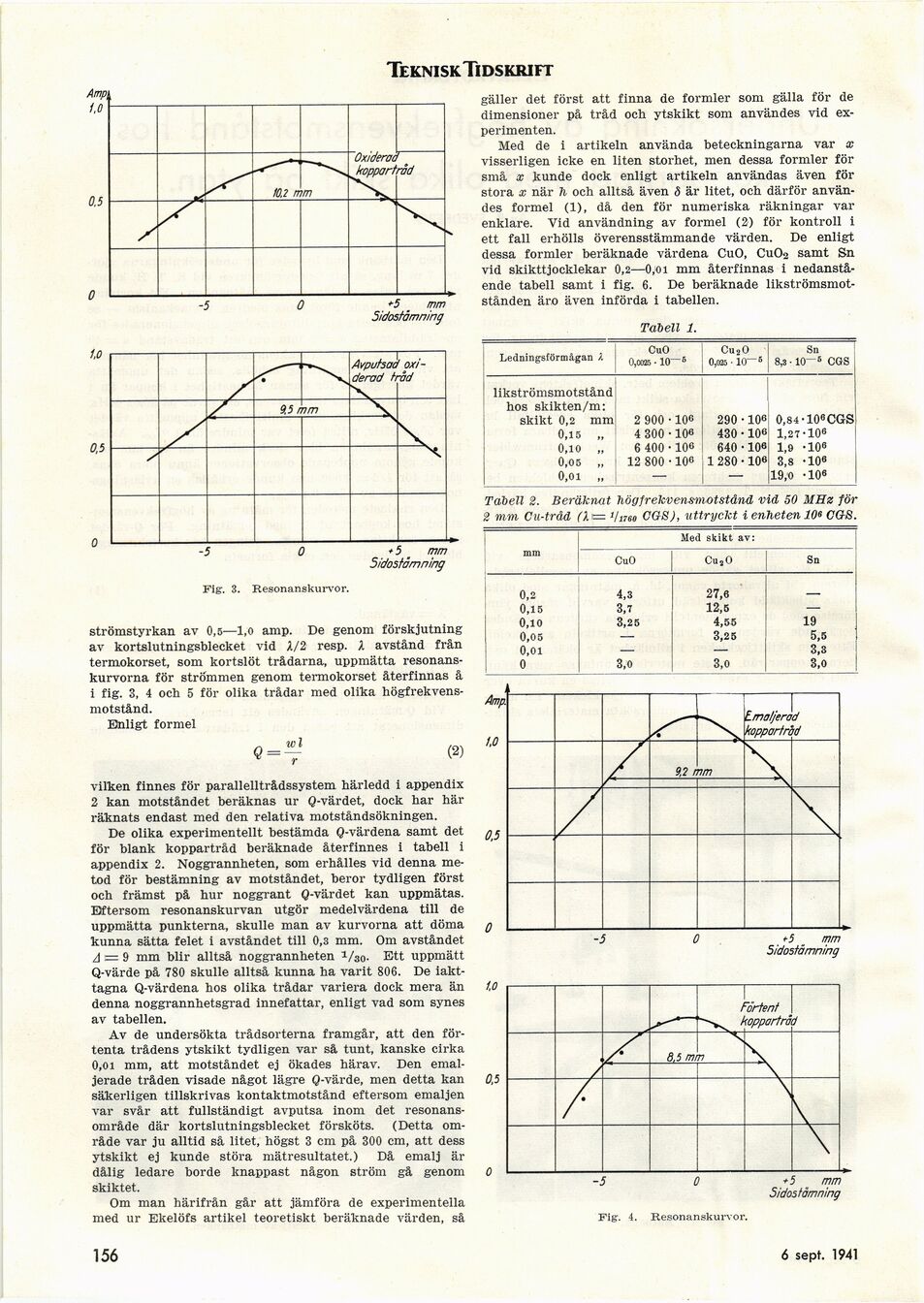
Fig. 3. Resonanskurvor.
strömstyrkan av 0,5—1,0 amp. De genom förskjutning
av kortslutningsblecket vid A/2 resp. X avstånd från
termokorset, som kortslöt trådarna, uppmätta
resonanskurvorna för strömmen genom termokorset återfinnas å
1 fig. 3, 4 och 5 för olika trådar med olika
högfrekvens-motstånd.
Enligt formel
= ^ (2)
vilken finnes för parallelltrådssystem härledd i appendix
2 kan motståndet beräknas ur O-värdet, dock har här
räknats endast med den relativa motståndsökningen.
De olika experimentellt bestämda Q-värdena samt det
för blank koppartråd beräknade återfinnes i tabell i
appendix 2. Noggrannheten, som erhålles vid denna
metod för bestämning av motståndet, beror tydligen först
och främst på hur noggrant Q-värdet kan uppmätas.
Eftersom resonanskurvan utgör medelvärdena till de
uppmätta punkterna, skulle man av kurvorna att döma
kunna sätta felet i avståndet till 0,3 mm. Om avståndet
A ~ 9 mm blir alltså noggrannheten i/30. Ett uppmätt
Q-värde på 780 skulle alltså kunna ha varit 806. De
iakttagna Q-värdena hos olika trådar variera dock mera än
denna noggrannhetsgrad innefattar, enligt vad som synes
av tabellen.
Av de undersökta trådsorterna framgår, att den
för-tenta trådens ytskikt tydligen var så tunt, kanske cirka
0,oi mm, att motståndet ej ökades härav. Den
emaljerade tråden visade något lägre Q-värde, men detta kan
säkerligen tillskrivas kontaktmotstånd eftersom emaljen
var svår att fullständigt avputsa inom det
resonansområde där kortslutningsblecket försköts. (Detta
område var ju alltid så litet, högst 3 cm på 300 cm, att dess
ytskikt ej kunde störa mätresultatet.) Då emalj är
dålig ledare borde knappast någon ström gå genom
skiktet.
Om man härifrån går att jämföra de experimentella
med ur Ekelöfs artikel teoretiskt beräknade värden, så
156
gäller det först att finna de formler som gälla för de
dimensioner på tråd och ytskikt som användes vid
experimenten.
Med de i artikeln använda beteckningarna var x
visserligen icke en liten storhet, men dessa formler för
små x kunde dock enligt artikeln användas även för
stora x när K och alltså även 5 är litet, och därför
användes formel (1), då den för numeriska räkningar var
enklare. Yid användning av formel (2) för kontroll i
ett fall erhölls överensstämmande värden. De enligt
dessa formler beräknade värdena CuO, Cu02 samt Sn
vid skikttjocklekar 0,2—0,oi mm återfinnas i
nedanstående tabell samt i fig. 6. De beräknade
likströmsmotstånden äro även införda i tabellen.
Tabell 1.
Ledningsförmågan X CuO 0,0025 - 10~5 Cu20 0,025 • 10—6 Sn 8,3-10—5 CGS
likströmsmotstånd hos skikten/m: skikt 0,2 mm 0,15 „ 0,io „ 0,05 „ 0,oi „ 2 900 • 10« 4 300 • 10« 6 400 • 106 12 800 • 106 290 • 106 430 • 106 640 • 106 1 280 • 106 0,84-100CGS 1,27 * 106 1,9 -108 3,8 -10« 19,0 -106
Tabell 2. Beräknat högfrekvensmotstånd vid 50 MHz för
2 mm Cu-tråd (Xi= ’/mo CGS), uttryckt i enheten lO» CQ-8.
mm Med skikt av:
CuO Cu20 Sn
0,2 4,3 27,6 _
0,15 3,7 12,5 —
0,10 3,25 4,55 19
0,05 — 3,25 5,5
0,01 — — 3,3
0 3,0 3,0 3,0
-5 0 +5 mm
Sidosfämning
Fig. 4. Resonanskurvor.
6 sept. 1941
<< prev. page << föreg. sida << >> nästa sida >> next page >>