
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
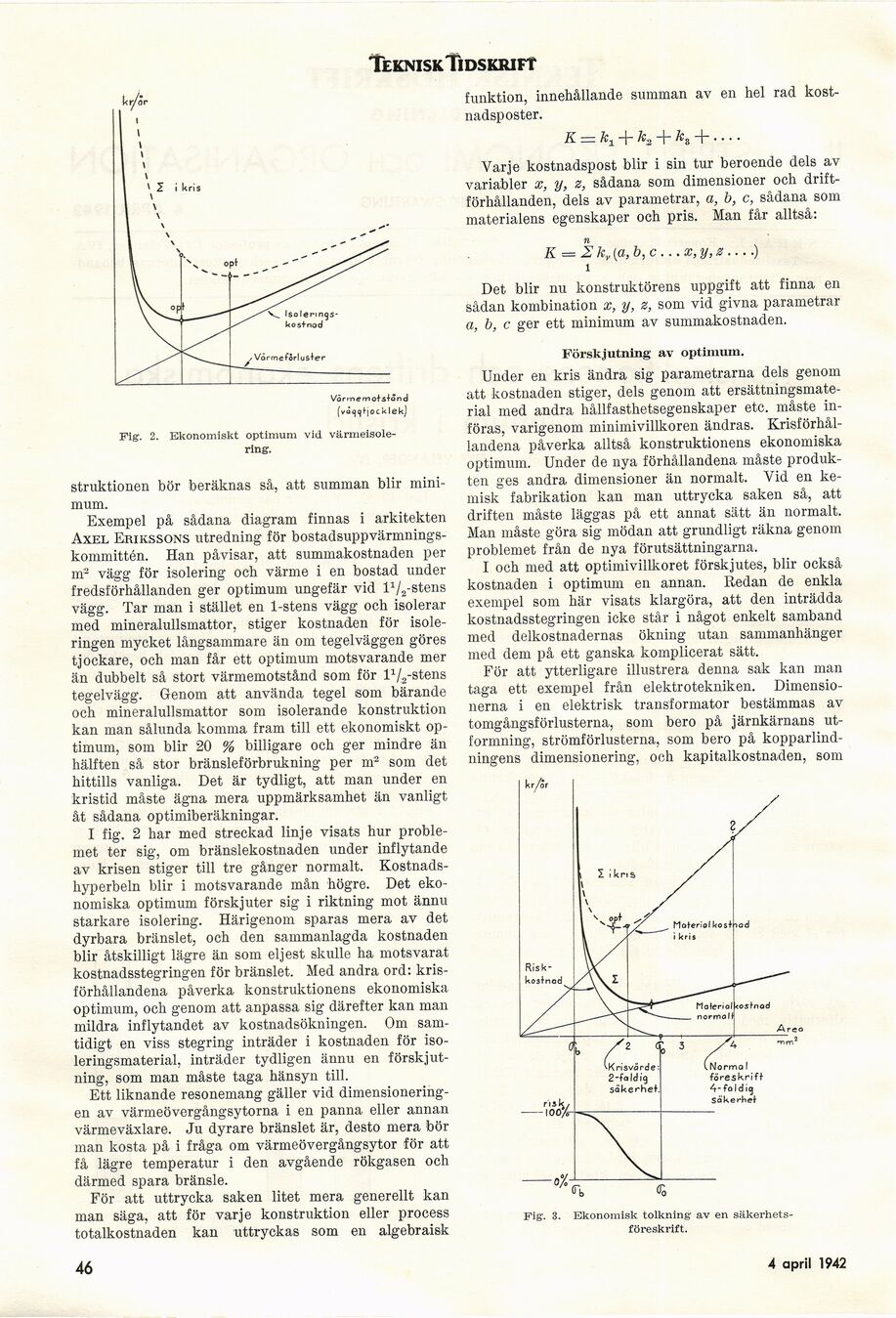
Vör memots+önd
(vàqqfjocklek)
Fig. 2. Ekonomiskt optimum vid
värmeisolering.
struktionen bör beräknas så, att summan blir
minimum.
Exempel på sådana diagram finnas i arkitekten
Axel Erikssons utredning för
bostadsuppvärmnings-kommittén. Han påvisar, att summakostnaden per
m2 vägg för isolering och värme i en bostad under
fredsförhållanden ger optimum ungefär vid l^-stens
vägg. Tar man i stället en 1-stens vägg och isolerar
med mineralullsmattor, stiger kostnaden för
isoleringen mycket långsammare än om tegelväggen göres
tjockare, och man får ett optimum motsvarande mer
än dubbelt så stort värmemotstånd som för l1/2-stens
tegelvägg. Genom att använda tegel som bärande
och mineralullsmattor som isolerande konstruktion
kan man sålunda komma fram till ett ekonomiskt
optimum, som blir 20 % billigare och ger mindre än
hälften så stor bränsleförbrukning per m2 som det
hittills vanliga. Det är tydligt, att man under en
kristid måste ägna mera uppmärksamhet än vanligt
åt sådana optimiberäkningar.
I fig. 2 har med streckad linje visats hur
problemet ter sig, om bränslekostnaden under inflytande
av krisen stiger till tre gånger normalt.
Kostnads-hyperbeln blir i motsvarande mån högre. Det
ekonomiska optimum förskjuter sig i riktning mot ännu
starkare isolering. Härigenom sparas mera av det
dyrbara bränslet, och den sammanlagda kostnaden
blir åtskilligt lägre än som eljest skulle ha motsvarat
kostnadsstegringen för bränslet. Med andra ord:
kris-förhållandena påverka konstruktionens ekonomiska
optimum, och genom att anpassa sig därefter kan man
mildra inflytandet av kostnadsökningen. Om
samtidigt en viss stegring inträder i kostnaden för
isoleringsmaterial, inträder tydligen ännu en
förskjutning, som man måste taga hänsyn till.
Ett liknande resonemang gäller vid
dimensioneringen av värmeövergångsytorna i en panna eller annan
värmeväxlare. Ju dyrare bränslet är, desto mera bör
man kosta på i fråga om värmeövergångsytor för att
få lägre temperatur i den avgående rökgasen och
därmed spara bränsle.
För att uttrycka saken litet mera generellt kan
man säga, att för varje konstruktion eller process
totalkostnaden kan uttryckas som en algebraisk
funktion, innehållande summan av en hel rad
kostnadsposter.
Ä = Ä1 + Å2 + ÄS + ....
Varje kostnadspost blir i sin tur beroende dels av
variabler x, y, z, sådana som dimensioner och
driftförhållanden, dels av parametrar, a, b, c, sådana som
materialens egenskaper och pris. Man får alltså:
n
K = 2 kv(a,b,c.. .x,y,z––)
i
Det blir nu konstruktörens uppgift att finna en
sådan kombination x, y, z, som vid givna parametrar
a, b, c ger ett minimum av summakostnaden.
Förskjutning av optimum.
Under en kris ändra sig parametrarna dels genom
att kostnaden stiger, dels genom att
ersättningsmaterial med andra hållfasthetsegenskaper etc. måste
införas, varigenom minimivillkoren ändras.
Krisförhållandena påverka alltså konstruktionens ekonomiska
optimum. Under de nya förhållandena måste
produkten ges andra dimensioner än normalt. Vid en
kemisk fabrikation kan man uttrycka saken så, att
driften måste läggas på ett annat sätt än normalt.
Man måste göra sig mödan att grundligt räkna genom
problemet från de nya förutsättningarna.
I och med att optimivillkoret förskjutes, blir också
kostnaden i optimum en annan. Redan de enkla
exempel som här visats klargöra, att den inträdda
kostnadsstegringen icke står i något enkelt samband
med delkostnadernas ökning utan sammanhänger
med dem på ett ganska komplicerat sätt.
För att ytterligare illustrera denna sak kan man
taga ett exempel från elektrotekniken.
Dimensionerna i en elektrisk transformator bestämmas av
tomgångsförlusterna, som bero på järnkärnans
utformning, strömförlusterna, som bero på
kopparlind-ningens dimensionering, och kapitalkostnaden, som
Fig. 3. Ekonomisk tolkning av en
säkerhetsföreskrift.
46
4 april 1942
<< prev. page << föreg. sida << >> nästa sida >> next page >>