
Full resolution (JPEG) - On this page / på denna sida - H. 35. 2 september 1944 - Ultrakorta vågors utbredning, av Ove Norell
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
1020
TEKNISK TIDSKRIFT
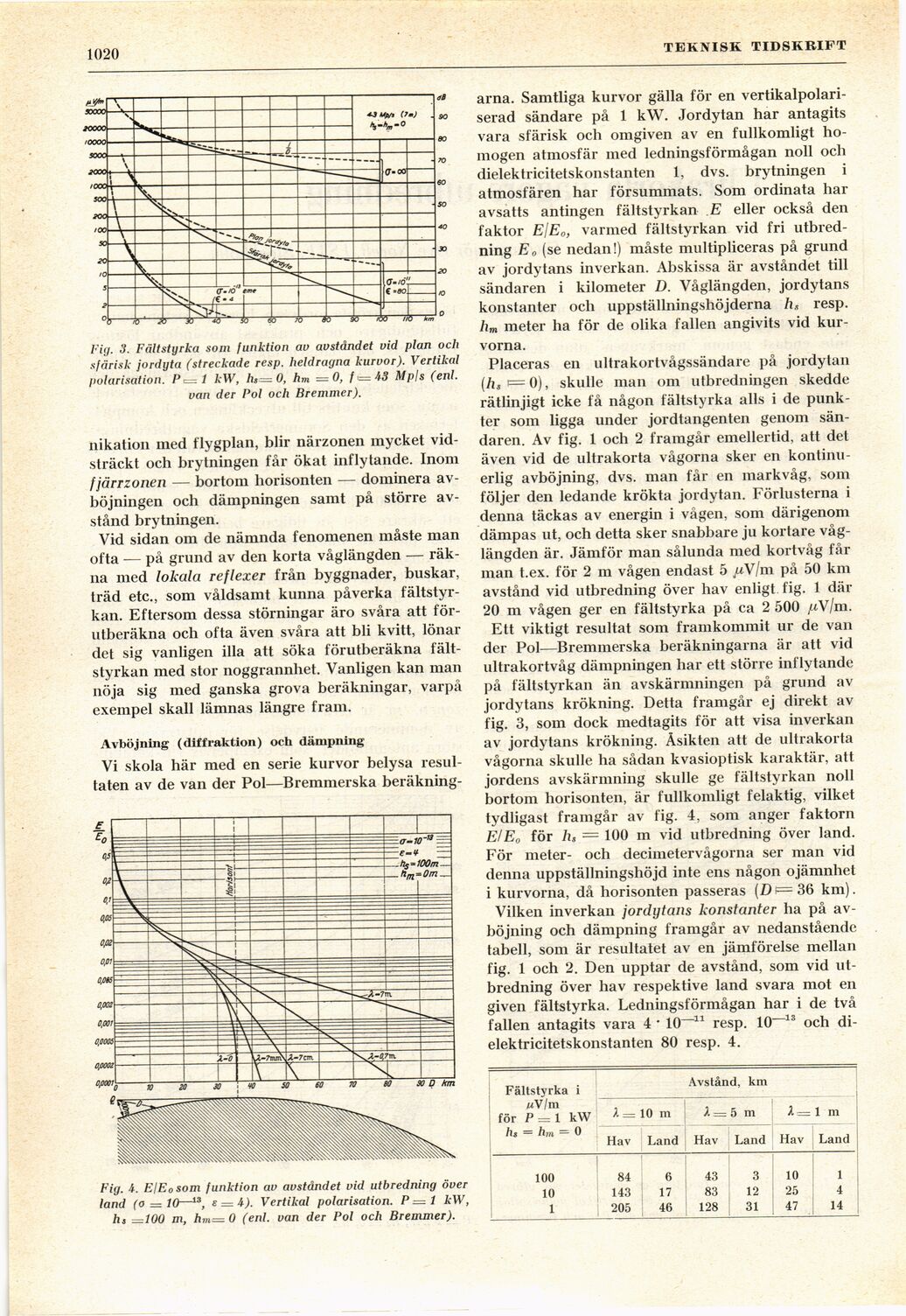
Fig. 3. Fältstyrka som funktion av avståndet vid plan och
sfärisk jordyta (streckade resp. heldragna kurvor). Vertikal
polarisation. Pa=l kW, hs=0, hm =0, f>=43 Mpls (enl.
van der Pol och Bremmer).
nikatioii med flygplan, blir närzonen mycket
vidsträckt och brytningen får ökat inflytande. Inom
fjärrzonen — bortom horisonten — dominera
avböjningen och dämpningen samt på större
avstånd brytningen.
Vid sidan om de nämnda fenomenen måste man
ofta — på grund av den korta våglängden —
räkna med lokala reflexer från byggnader, buskar,
träd etc., som våldsamt kunna påverka
fältstyrkan. Eftersom dessa störningar äro svåra att
förutberäkna och ofta även svåra att bli kvitt, lönar
det sig vanligen illa att söka förutberäkna
fältstyrkan med stor noggrannhet. Vanligen kan man
nöja sig ined ganska grova beräkningar, varpå
exempel skall lämnas längre fram.
Avböjning (diffraktion) och dämpning
Vi skola här med en serie kurvor belysa
resultaten av de van der Pol—Bremmerska beräkning-
Fig. i. E/E0 som funktion av avståndet vid utbredning över
land (o — 10—13, s — 4). Vertikal polarisation. P —i kW,
hs —100 m, hm=0 (enl. van der Pol och Bremmer).
arna. Samtliga kurvor gälla för en
vertikalpolari-serad sändare på 1 kW. Jordytan har antagits
vara sfärisk och omgiven av en fullkomligt
homogen atmosfär med ledningsförmågan noll och
dielektricitetskonstanten 1, dvs. brytningen i
atmosfären har försummats. Som ordinata har
avsatts antingen fältstyrkan E eller också den
faktor EIE o, varmed fältstyrkan vid fri
utbredning E0 (se nedan!) måste multipliceras på grund
av jordytans inverkan. Abskissa är avståndet till
sändaren i kilometer D. Våglängden, jordytans
konstanter ocli uppställningshöjderna hs resp.
hm meter ha för de olika fallen angivits vid
kurvorna.
Placeras en ultrakortvågssändare på jordytan
(hs*=0), skulle man om utbredningen skedde
rätlinjigt icke få någon fältstyrka alls i de
punkter som ligga under jordtangenten genom
sändaren. Av fig. 1 och 2 framgår emellertid, att det
även vid de ultrakorta vågorna sker en
kontinuerlig avböjning, dvs. man får en markvåg, som
följer den ledande krökta jordytan. Förlusterna i
denna täckas av energin i vågen, som därigenom
dämpas ut, och detta sker snabbare ju kortare
våglängden är. Jämför man sålunda med kortvåg får
man t.ex. för 2 m vågen endast 5 jwV/m på 50 km
avstånd vid utbredning över hav enligt fig. 1 där
20 m vågen ger en fältstyrka på ca 2 500 /tV/m.
Ett viktigt resultat som framkommit ur de van
der Pol—Bremmerska beräkningarna är att vid
ultrakortvåg dämpningen har ett större inflytande
på fältstyrkan än avskärmningen på grund av
jordytans krökning. Detta framgår ej direkt av
fig. 3, som dock medtagits för att visa inverkan
av jordytans krökning. Åsikten att de ultrakorta
vågorna skulle ha sådan kvasioptisk karaktär, att
jordens avskärmning skulle ge fältstyrkan noll
bortom horisonten, är fullkomligt felaktig, vilket
tydligast framgår av fig. 4, som anger faktorn
E/E0 för hs = 100 m vid utbredning över land.
För meter- och decimetervågorna ser man vid
denna uppställningshöjd inte ens någon ojämnhet
i kurvorna, då horisonten passeras (D i= 36 km).
Vilken inverkan jordytans konstanter ha på
avböjning och dämpning framgår av nedanstående
tabell, som är resultatet av en jämförelse mellan
fig. 1 och 2. Den upptar de avstånd, som vid
utbredning över hav respektive land svara mot en
given fältstyrka. Ledningsförmågan har i de två
fallen antagits vara 4 • 10—11 resp. lO–13 och
dielektricitetskonstanten 80 resp. 4.
Fältstyrka i tiVl m för P = 1 kW hs = hin — 0 Avstånd, km
X — 10 m X:= 5 m X = 1 m
Hav Land Hav Land Hav Land
100 84 6 43 3 10 1
10 143 17 83 12 25 4
1 205 46 128 31 47 14
<< prev. page << föreg. sida << >> nästa sida >> next page >>