
Full resolution (JPEG) - On this page / på denna sida - H. 16. 22 april 1950 - Värmeöverföring genom gasstrålning, av Torsten Widell
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
.366
TEKNISK TIDSKRIFT
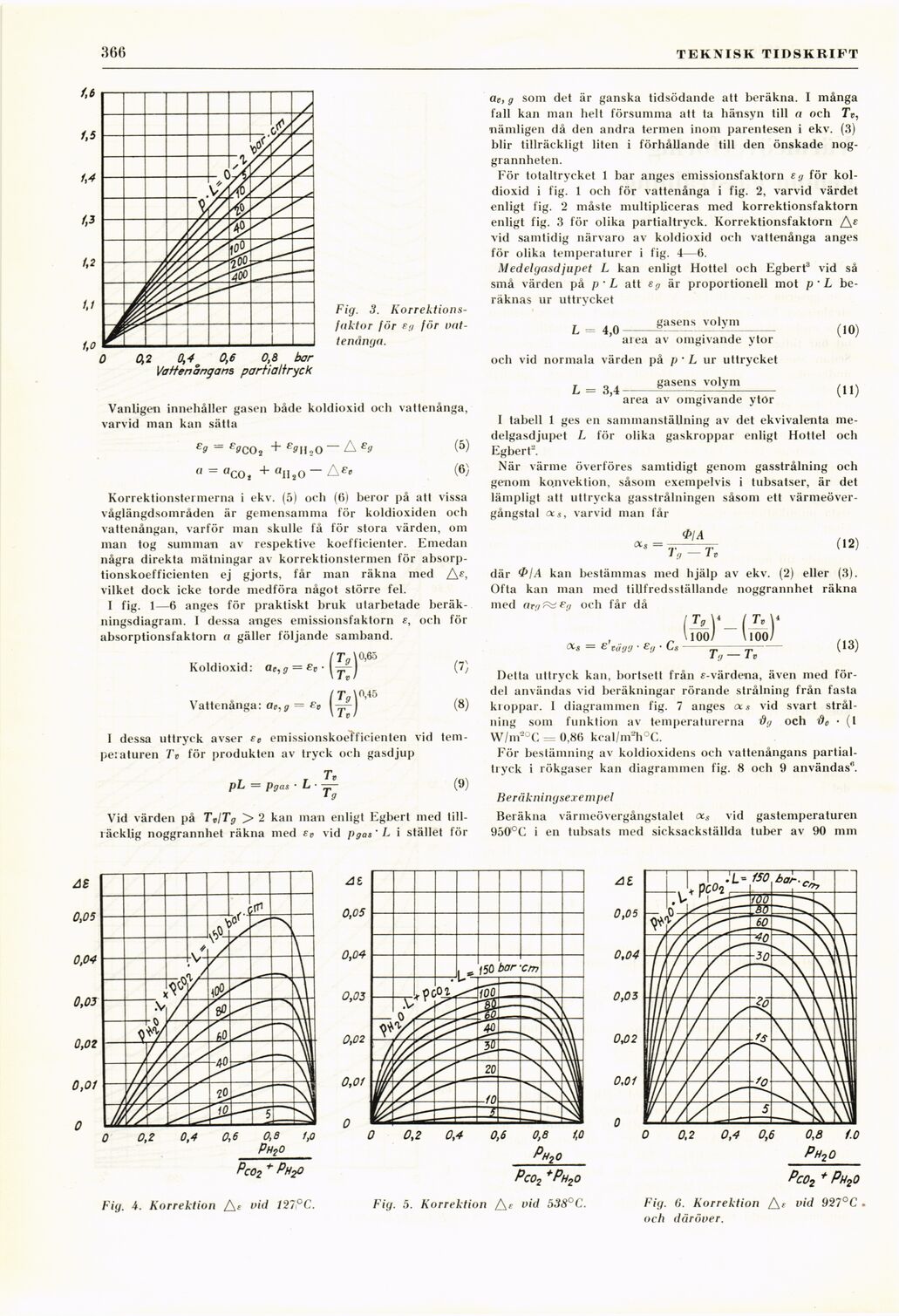
Fig. 3.
Korrektions-faktor för Fr) för
vattenånga.
Vanligen innehåller gasen både koldioxid och vattenånga,
varvid man kan sätta
fCO,
+ £
SHoO
— Aeg
4- a
IIoO
— A c»
(5)
(6)
Korrektionstermerna i ekv. (5) och (6) beror på att vissa
våglängdsområden är gemensamma för koldioxiden och
vattenångan, varför man skulle få för stora värden, om
man tog summan av respektive koefficienter. Emedan
några direkta mätningar av korrektionstermen för
absorptionskoefficienten ej gjorts, får man räkna med Af,
vilket dock icke torde medföra något större fel.
I fig. 1—6 anges för praktiskt bruk utarbetade
beräk-ningsdiagram. 1 dessa anges emissionsfaktorn s, och för
absorptionsfaktor!! a gäller följande samband.
/ T g \°>’
Koldioxid: ae, g = Sv • ^-=~J
(TgW
Vattenanga: av, g = ^y-J
(7)
(8)
I dessa uttryck avser ee emissionskoetficienten vid
temperaturen Tv för produkten av tryck och gasdjup
T,
pL = Pgas • L •
(9)
Vid värden på TtITg > 2 kan man enligt Egbert med
tillräcklig noggrannhet räkna med sv vid pga»’ L i stället för
ae, g som det är ganska tidsödande att beräkna. 1 många
fall kan man helt försumma att ta hänsyn till a och TV,
nämligen då den andra termen inom parentesen i ekv. (3)
blir tillräckligt liten i förhållande till den önskade
noggrannheten.
För totaltrycket 1 bar anges emissionsfaktorn sg för
koldioxid i fig. 1 och för vattenånga i fig. 2, varvid värdet
enligt fig. 2 måste multipliceras med korrektionsfaktorn
enligt fig. 3 för olika partialtryck. Korrektionsfaktorn Ac
Aid samtidig närvaro av koldioxid och vattenånga anges
för olika temperaturer i fig. 4—6.
Medelgasdjupet L kan enligt Hottel och Egbert3 vid så
små värden på p * L att sg är proportionell mot p’L
beräknas ur uttrycket
L = 4,0
gasens volym
(10)
aiea av omgivande ytor
och vid normala värden på p ’ L ur uttrycket
L = 3,4-gasens volym
area av omgivande ytor
I tabell 1 ges en sammanställning av det ekvivalenta
medelgasdjupet L för olika gaskroppar enligt Hottel och
Egbert2.
När värme överföres samtidigt genom gasstrålning och
genom konvektion, såsom exempelvis i tubsatser, är det
lämpligt att uttrycka gasstrålningen såsom ett
värmeövergångstal ex.s, varvid man får
lg - 1 v
där &IA kan bestämmas med hjälp av ekv. (2) eller (3).
Ofta kan man med tillfredsställande noggrannhet räkna
med av/f^Fg och får då
(Tg_\
— vä(j’j ’ £’/ • Cs
\ 100/
\ 100/
Tg — Tv
(13)
Detta uttryck kan, bortsett från e-värdena, även med
fördel användas vid beräkningar rörande strålning från fasta
kroppar. 1 diagrammen fig. 7 anges cxs vid svart
strålning som funktion av temperaturerna äg och d„ • (l
W/nr°C = 0,80 kcal/nrh°C.
För bestämning av koldioxidens och vattenångans
partial-tryck i rökgaser kan diagrammen fig. 8 och 9 användas".
Beräkningsexempel
Beräkna värmeövergångstalet ocs vid gastemperaturen
950°C i en tubsats med sicksackställda tuber av 90 mm
Fig. 4. Korrektion A* vid 727,°C.
Fig. 5. Korrektion A* vid 538°C.
Fig. 6. Korrektion Af vid 927°C
och däröver.
<< prev. page << föreg. sida << >> nästa sida >> next page >>