
Full resolution (JPEG) - On this page / på denna sida - H. 26. 30 juni 1953 - Mekaniska räkneelement i luftvärnets eldledningsutrustning, av Gunnar Engdahl
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
16 juni 1953
543
derivator. I praktiken kommer dock dels på
grund av ofrånkomliga pendlingar i
mätelemen-ten genom ofullkomliga riktmetoder dels på
grund av inuti instrumentet uppstående
ytterligare pendlingar på grund av mekaniska
toleranser förstaderivatorna ej att vara konstanta
utan överlagras med svängningar även om målet
rör sig under exakt konstant rörelsetillstånd.
Dessa svängningar måste utjämnas och för detta
ändamål utnyttjas utjämningskretsar med
tidskonstanter av varierande längder.
I elektriska instrument är det lätt att t.ex.
genom olika integreringskretsar erhålla olika
tidskonstanter, medan i de mekaniska instrumenten
endast en tidskonstant i allmänhet kan
utnyttjas. Denna erhålles t.ex. i det tidigare skisserade
instrumentet ur tröghetsmomenten och
massorna hos de rörliga delarna i derivatorn fig. 14.
Gammainstrumentet har även en utjämning vid
bestämning av målets kursbäring. Denna ligger
i mätrullen (fig. 3) och representeras av
avståndet mellan hjulets anliggningspunkt och
vertikala vridningsaxeln projektion på basplattan —
stort avstånd ger god utjämning och vice versa.
Valet av utjämningstid är av mycket stor
betydelse i ett eldledningsinstrument. I ett diagram
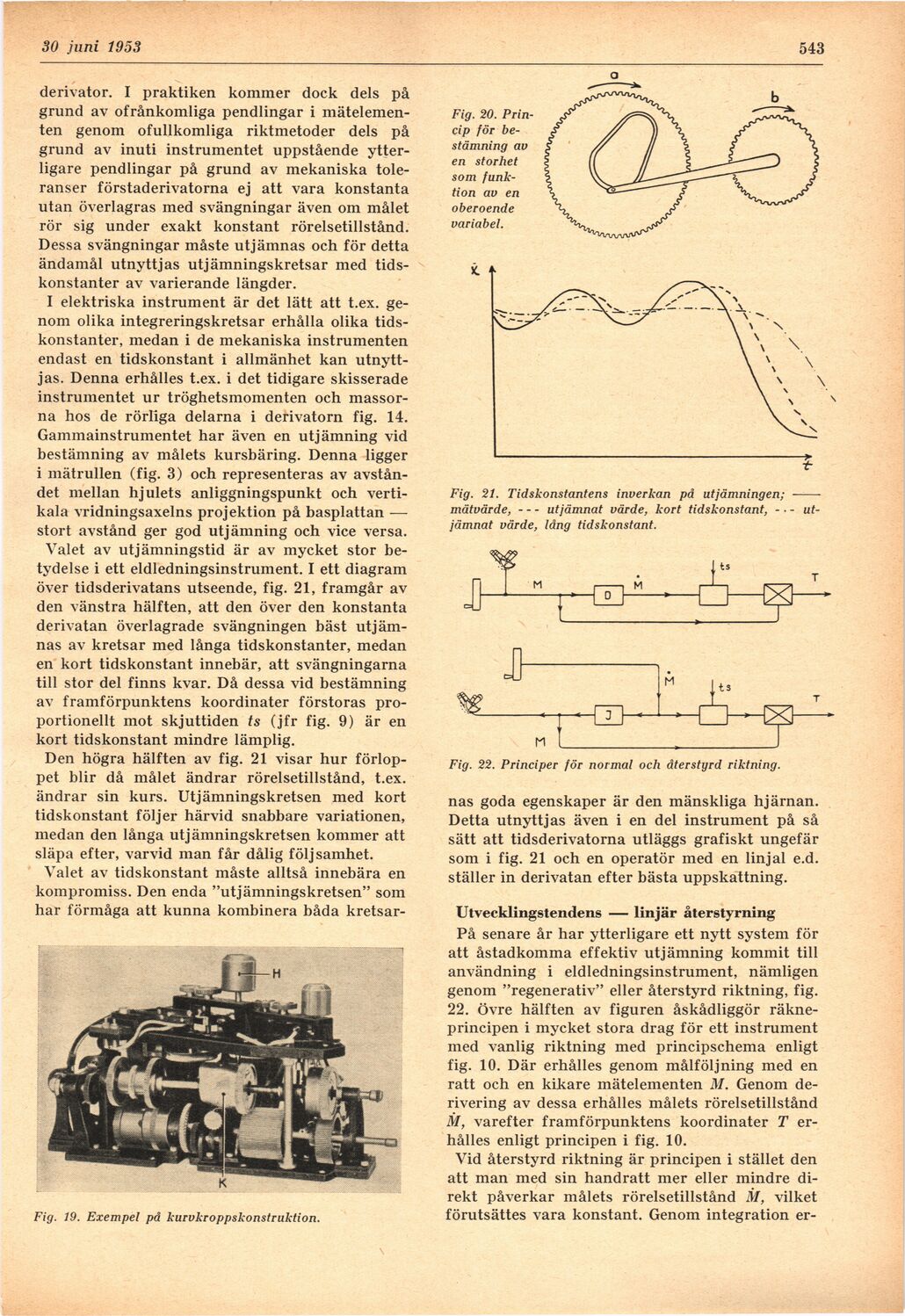
över tidsderivatans utseende, fig. 21, framgår av
den vänstra hälften, att den över den konstanta
derivatan överlagrade svängningen bäst
utjämnas av kretsar med långa tidskonstanter, medan
en kort tidskonstant innebär, att svängningarna
till stor del finns kvar. Då dessa vid bestämning
av framförpunktens koordinater förstoras
proportionellt mot skjuttiden ts (jfr fig. 9) är en
kort tidskonstant mindre lämplig.
Den högra hälften av fig. 21 visar hur
förloppet blir då målet ändrar rörelsetillstånd, t.ex.
ändrar sin kurs. Utjämningskretsen med kort
tidskonstant följer härvid snabbare variationen,
medan den långa utjämningskretsen kommer att
släpa efter, varvid man får dålig följsamhet.
Valet av tidskonstant måste alltså innebära en
kompromiss. Den enda "utjämningskretsen" som
har förmåga att kunna kombinera båda kretsar-
Fig. 19. Exempel på kurvkroppskonstruktion.
Fig. 20.
Princip för
bestämning av
en storhet
som
funktion av en
oberoende
variabel.
Fig. 21. Tidskonstantens inverkan på utjämningen; -
mätvärde,–-utjämnat värde, kort tidskonstant, —
utjämnat värde, lång tidskonstant.
Fig. 22. Principer för normal och återstyrd riktning.
nas goda egenskaper är den mänskliga hjärnan.
Detta utnyttjas även i en del instrument på så
sätt att tidsderivatorna utläggs grafiskt ungefär
som i fig. 21 och en operatör med en linjal e.d.
ställer in derivatan efter bästa uppskattning.
Utvecklingstendens — linjär återstyrning
På senare år har ytterligare ett nytt system för
att åstadkomma effektiv utjämning kommit till
användning i eldledningsinstrument, nämligen
genom "regenerativ" eller återstyrd riktning, fig.
22. övre hälften av figuren åskådliggör
räkne-principen i mycket stora drag för ett instrument
med vanlig riktning med principschema enligt
fig. 10. Där erhålles genom målföljning med en
ratt och en kikare mätelementen M. Genom
de-rivering av dessa erhålles målets rörelsetillstånd
M, varefter framförpunktens koordinater T
erhålles enligt principen i fig. 10.
Vid återstyrd riktning är principen i stället den
att man med sin handratt mer eller mindre
direkt påverkar målets rörelsetillstånd M, vilket
förutsättes vara konstant. Genom integration er-
<< prev. page << föreg. sida << >> nästa sida >> next page >>