
Full resolution (JPEG) - On this page / på denna sida - 1959, H. 21 - Skorstenars dynamiska stabilitet, av Johan F Hagerup och Nils-Erik Bronner
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
att skorstenen kan uthärda en
resonanssvängning.
Uppdelning i alternativ 1 och 2 förutsätter att
virvelavlösningsfrekvensen följer von Kårmåns
formel. Skulle i stället virvelavlösningen styras
av skorstenens egensvängningar (grundtonen)
finnes som förut nämnts ingen utpräglad
resonanspunkt, vilket medför, att man i båda fallen
bör göra en kontroll av stabiliteten under
förutsättning av resonanssvängning vid högsta
vindstyrka, varvid man enligt Ozker och Smith
sätter CL = 0,2.
Vare sig svängningarna har karaktären av att
vara antingen påtvingade eller självmatade är
alternativ i att föredra, eftersom det alltid ger
en styvare skorsten som lättare kan
dimensioneras för att uthärda en resonanssvängning
vid högsta vindstyrka.
Emellertid skulle dimensionering i enlighet
med alternativ 1 i många fall leda till en
mycket kraftig ökning av skorstensdiametern i
förhållande till vad som erfordras med hänsyn
till skorstenens funktion.
Egenfrekvensen f (i Hz) för en i ena änden
fast inspänd stav med konstant tvärsnitt
beräknas enligt formeln
2n V I3
Ely
Q
(10)
där C beror på svängningsformen, varvid C0 —
= 3,52 för grundtonen och Cx = 22,0 för första
övertonen; Q är stavens totala tyngd.
En skorsten torde dock sällan ha formen av
en stav med konstant tvärsnitt. För att
underlätta beräkningen av i praktiken
förekommande fall har en generell formel härletts för
beräkning av grundtonen för en stav sammansatt
av två delar med var för sig konstanta
tvärsnitt, fig. 5. Beräkningen har utförts med hjälp
av Lörd Rayleigh’s approximativa metod3. Felet
i beräkningen torde ligga vid ca 1 %.
För beräkningen har följande beteckningar
använts:
y (El) 2’
där Q är stavens tyngd, E elasticitetsmodul, I
tröghetsmoment och l längd; index 1 avser
nedre delen och 2 övre delen.
Grundfrekvensen n erhålles ur
där
K = 1,97
„ 3,52 1 /(El) ty
" = k-2xT W
. j/ (x> y>z)
(ii)
ft (x, z) + x- fi (x, y, z)
Funktionerna i ekv. (12) är följande:
fi (x, y, z) = 3x2 z2 + 6x2 z + 2xz + 4x2 + 3x +
(12)
_L 6 JL 6 2 i
+ 1Ö+1ÖX ^
h (x, z) - ^ (1 + x)2 + ^ (1 + 2x + xz)2
-7 5
■8(1 + x)(l + 2x + xz) +y(l + 2x + xz)-
8
(13)
lOz2
h (x. ;/, z) = (3 + 8x + 6*z)* + — (1 + 3x + 3xz)» +
104
+ -rr- x2y2z« + 4z (1 + 3x + 3xz) (3 + 8x + 6xz) + 2 xyz3
45
[fe
52 z
+ Sx + 6 xz) + — (1 + 3x + 3xz
15
)] (15)
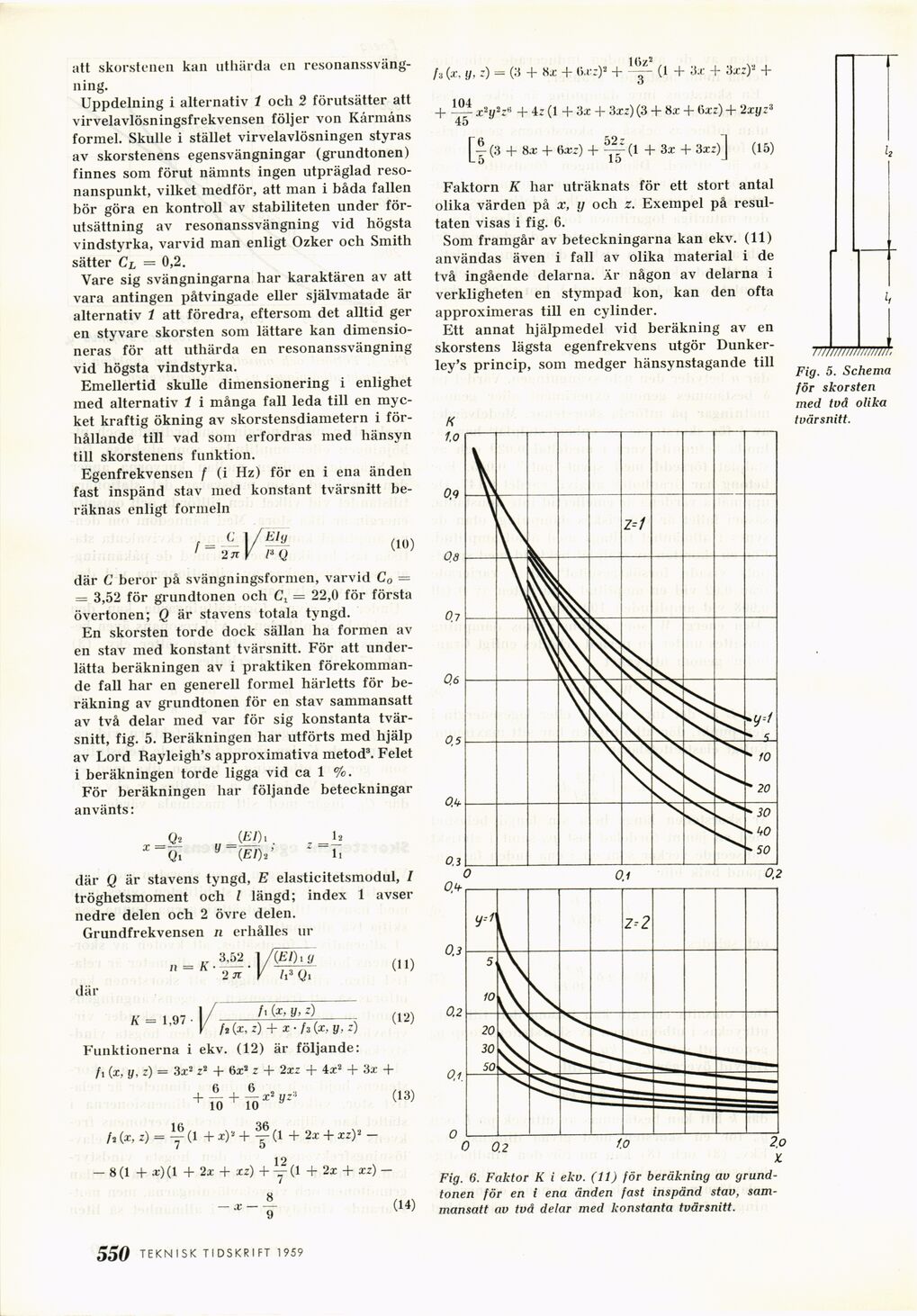
Faktorn K har uträknats för ett stort antal
olika värden på x, y och z. Exempel på
resultaten visas i fig. 6.
Som framgår av beteckningarna kan ekv. (11)
användas även i fall av olika material i de
två ingående delarna. Är någon av delarna i
verkligheten en stympad kon, kan den ofta
approximeras till en cylinder.
Ett annat hjälpmedel vid beräkning av en
skorstens lägsta egenfrekvens utgör
Dunker-ley’s princip, som medger hänsynstagande till
(14)
Fig. 6. Faktor K i eko. (11) för beräkning av
grundtonen för en i ena änden fast inspänd stav,
sammansatt av två delar med konstanta tvärsnitt.
Fig. 5. Schema
för skorsten
med två olika
tvärsnitt.
550 TEKNISK TIDSKRIFT 1959
<< prev. page << föreg. sida << >> nästa sida >> next page >>