
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
152
böra finna, om vi i eqv. (3) ponera y constant. Denna curvas
tangent i den nyssnämnde punkten gör vidare med linien en vinkel
a, hvars trigonometriska tangent, såsom vi lätt inse, bör erhållas,
om vi differentiera z i afseende på x under antagande, att y är
constant, således
df
tgft = dx’
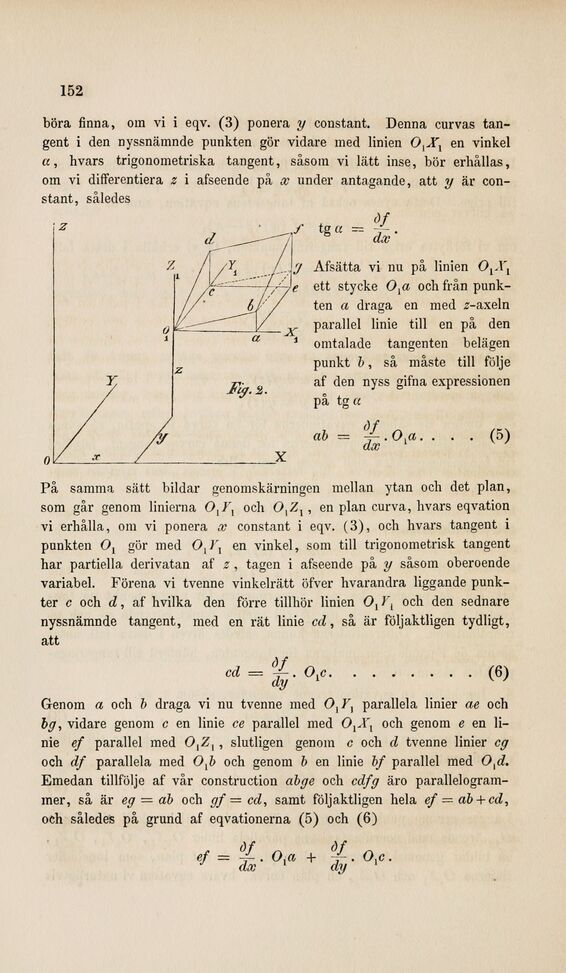
Afsätta vi nu på linien OlXl
ett stycke Oxa och från
punkten a draga en med «-axeln
parallel linie till en på den
omtalade tangenten belägen
punkt b, så måste till följe
af den nyss gifna expressionen
på tg a
ab = 0,a. . . . (5)
dx 1
På samma sätt bildar genomskärningen mellan ytan och det plan,
som går genom linierna O,i’, och , en plan curva, hvars eqvation
vi erhålla, om vi ponera x constant i eqv. (3), och hvars tangent i
punkten Ol gör med O,i\ en vinkel, som till trigonometrisk tangent
har partiella derivatan af z , tagen i afseende på y såsom oberoende
variabel. Förena vi tvenne vinkelrätt öfver hvarandra liggande
punkter c och d, af hvilka den förre tillhör linien O, >] och den sednare
nyssnämnde tangent, med en rät linie cd, så är följaktligen tydligt,
att
cd = 0,c........(6)
Genom a och b draga vi nu tvenne med OtFt parallela linier ae och
bg, vidare genom c en linie ce parallel med 0{Å\ och genom e en
linie ef parallel med 0,Z,, slutligen genom c och cl tvenne linier cg
och df parallela med Otb och genom b en linie bf parallel med Otd.
Emedan tillfölje af vår construction abge och cdfg äro
parallelogrammer, så är eg = ab och gf — cd, samt följaktligen hela ef = ab + cd,
och således på grund af eqvationerna (5) och (6)
<< prev. page << föreg. sida << >> nästa sida >> next page >>