Handledning uti nivelleringskonsten / 126-127 (1853) Author: Adolf Helander Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (JPEG) - On this page / på denna sida - §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

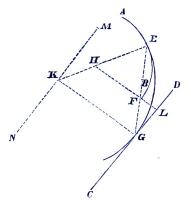Fig. 65

                        Om öfvergångspunkten E är gifven:

Sammanbind HE och drag ifrån H, eller den gifna bågens
medelpunkt, en rät linie HL vinkelrät emot CD; punkten F, hvari denna
linie skär bågen AB (förlängd om så behöfves), sammanbindes nu
med E och linien utdrages till dess den råkar CD i G, då denna
blir den andra öfvergångspunkten. Drag derefter ifrån G en rät
linie GK vinkelrät emot CD till dess den råkar den förlängda EH
uti K, så blir K medelpunkten för sammanbindningsbågen, hvilken
sednare tangerar bågen AB uti E och linien CD uti G.

                        Om öfvergångspunkten G är gifven:

Drag äfven i detta fall HL vinkelrät emot CD, så blir F,
såsom förut, bestämd, och sammanbind G med F samt utdrag linien
till E, så blir den andra öfvergångspunkten känd. Medelpunkten K
erbålles derefter såsom redan är visadt.

                        Om föreningsbågens radie är gifven:

Sätt denna radie = R och drag MN (fig. 65) parallel med
CD, så att afståndet dem emellan är = R. Sätt vidare bågens AB
radie = r och beskrif ur H med en radie = R – r en cirkel, som
afskär MN uti punkten K, som då blir föreningsbågens medelpunkt. Räta
linien KH utdragen bestämmer då ena öfvergångspunkten E, och
KG, vinkelrät emot CD, utvisar andra öfvergångspunkten G.

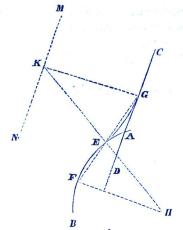Fig. 66.

Skulle (fig. 66) CD hafva en sådan direktion, att densamma
utdragen skulle skära den gifna bågen, så kommer föreningsbågens
medelpunkt att ligga åt motsatt sida. Om öfvergångspunkten E här
vore bestämd, så drag HF vinkelrät mot den förlängda CD, så
erbålles punkten F, hvilken sammanbindes med E och linien utdrages
till dess man får andra öfvergångspunkten G bestämd. Derifrån
drages GK vinkelrät mot CD, och punkten K, föreningsbågens
medelpunkt, erhålles om HE utdrages rätt fram till dess den råkar
GK. Är öfvergångspunkten G i stället gifven, så erhålles den
andra öfvergångspunkten E aldeles såsom i det föregående är visadt,
och likaså medelpunkten K. Är föreningsbågens radie, = R, gifven,
så drag MN parallel med CD och med vinkelrätt afstånd = R, samt
beskrif med H till medelpnnkt och en radie = R + r en cirkel, som
skär MN uti K, hvilken punkt då blir föreningsbågens medelpunkt.

7:o. Att sammanbinda tvenne cirkelformiga banor.

Fig. 67.[1]

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>