
Full resolution (TIFF) - On this page / på denna sida - Fjerde Boken. XII Proposition. Problem - Fjerde Boken. XIII Proposition. Problem
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
122
Fjerde Boken.
E A, b; så skall det bevisas, att ABCDE är en
regulier femhörning.
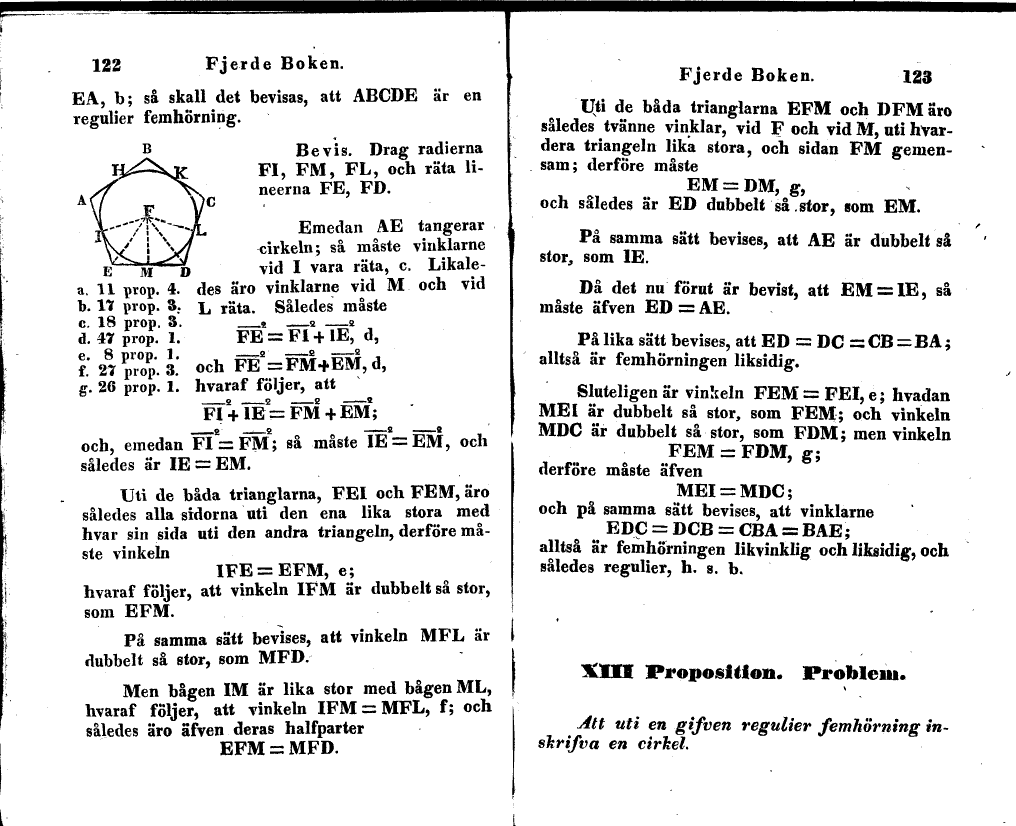
Bevis. Drag radierna FI, FM, FL, och räta lineerna
FE, FD.
Emedan AE tangerar cirkeln; så måste vinklarne
vid I vara räta, c, Likaledes äro vinklarne vid M
och vid L räta. Således måste
FE2=Fl2+"lEj d,
och FE2=FM^EM,d, hvaraf följer, att
E M
a. 11 prop. 4
b. 17 prop. S;
c. 18 prop. S
d. 47 prop. l
e. 8 prop. l
f. 27 prop. 3
g. 26 prop. l
och, emedan Ff2=: FM ; så måste TE^EM, och således
är IE = EM.
Uti de båda trianglarna, FEI och FEM, äro således alla
sidorna uti den ena lika stora med hvar sin sida uti
den andra triangeln, derföre måste vinkeln
IFE = EFM, e;
hvaraf följer, att vinkeln IF M är dubbelt så stor,
som EFM.
Få samma sätt bevises, att vinkeln MFL är dubbelt så
stor, som MFD.
Men bågen IM är lika stor med bågen ML, hvaraf
följer, att vinkeln IFM = MFL, f; och således äro
äfven deras halfparter EFM =: MFD.
Fjerde Boken.
123
Uti de båda trianglarna EFM och DFM äro således tvänne
vinklar, vid F och vid M, uti hvardera triangeln lika
stora, och sidan FM gemensam; derföre måste
EM = DM, g, och således är ED dubbelt så , stor,
som EM.
På samma sätt bevises, att AE är dubbelt så stor,
som 1E.
Då det nu förut är bevist, att EM = 1E, så måste
äfven ED = AE.
På lika sätt bevises, att ED = DC = CB - BÄ; alltså
är femhörningen liksidig.
Sluteligen är vinkeln FEM = FEI, e; hvadan ME I är
dubbelt så stor, som FEM; och vinkeln MDC är dubbelt
så stor, som FDM; men vinkeln
derföre måste äfven
MEI = MDC; och på samma sätt bevises, att vinklarne
EDC = DCB = CBA = BAB ; alltså är femhörningen
likvinkliga och liksidig, och således regulier, h,
s. b.
Proposition. Problem.
Att uti en gifven regulier femhörning inskrifva
en cirkel.
<< prev. page << föreg. sida << >> nästa sida >> next page >>