
Full resolution (TIFF) - On this page / på denna sida - Sjette Boken. XXIV Proposition. Theorem - Sjette Boken. XXV Proposition. Problem - Sjette Boken. XXVI Proposition. Theorem
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
188
Sjette Boken.
Men de rätlinige figurer, som äro likformige med en
och samma figur, äro sinsimellan likformige; derföre
är parallelogrammen GE likformig med KH5 h. s. b. (21
prop. 6.).
!%ÄY Proposition. Problem.
Alt upprita en rätlinig figur , som ctr likformig
med en gifven rätlinig figur, och lika sior rned en
annan gifven rätlinig figur.
Att upprita en figur, som är likformig med A och lika
stor med B.
Man applicerar till CD en parallelogram ED L - A, och
till DF en parallelogram FG-B, så att vinkeln GDF =3
DCE, a, Derigenom komma CD och DG uti en rät linea,
samt EF och FH uti en rät linea; b.
Nu söker man medleröta proportionalen, KL, till CD
och DG, c, och uppritar på KL en figur, M,
som är likformig med A, och lika ställd på KL, som
A är ställd på CD, d: det skall då bevisas, att M = B.
a. 45 prop. 1. Bevis. Ty då CD:KL = KL:DG;
b. 14 prop. 1. så måste .... A:M-CD:DG e.
c. 13 prop. 6. Men ..... CD:DG:=ED:FG f
e l Cor.Ull derföre är ... A:M = ED.FG; g
20 prop. 6. och då vi gjort . . A = ED,
f. l prop. 6. så måste ...... M = FG . . h.
g. 11 prop. 5. Men FG är gjord =: B;
derföre h. H prop. 5. mågte M = B h g b
_ F H K
Sjette Boken.
189
Proposition. TlaeoreAu
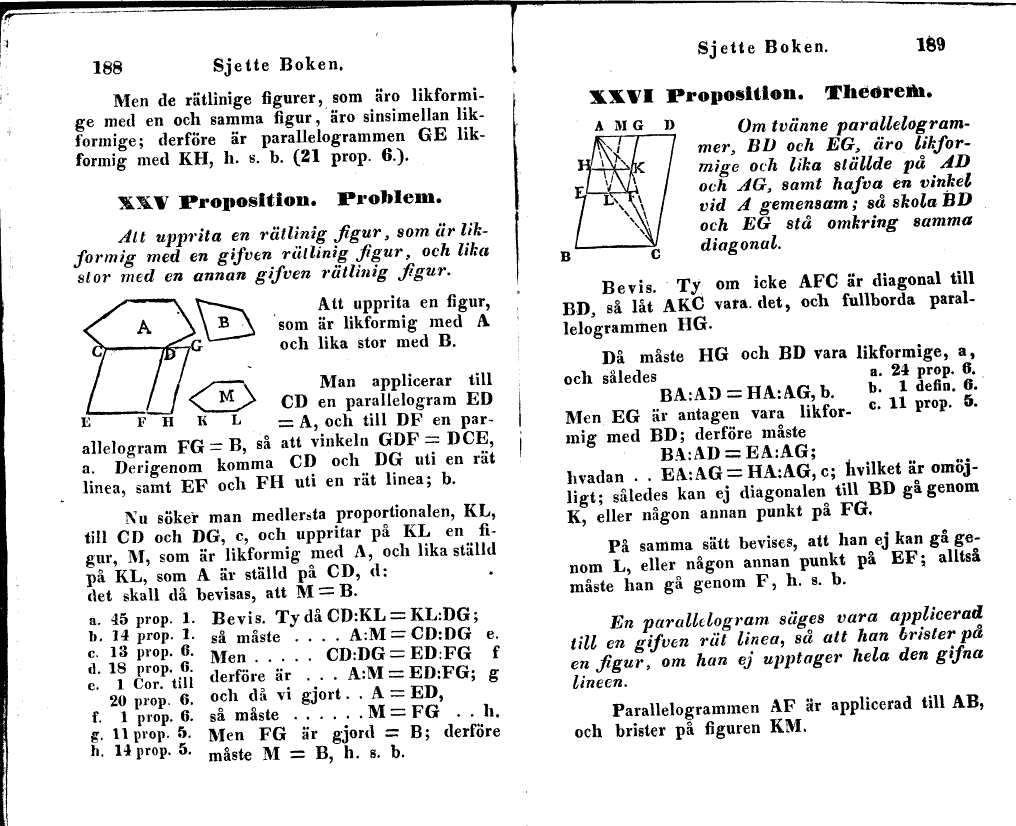
Om tvänne parallelogrammer, BD och EG, äro likformige
och lika ställde på AD och ÄG, samt hafva en vinkel
vid A gemensam; så skola BD och EG stå omkring samma
diagonal.
Bevis. Ty om icke AFC är diagonal till BD, så låt
AKC vata, det, och fullborda parallelogrammen HG.
Då måste HG och BD vara likformige, a, och således
a. 24 prop. 6.
BA:AD = HA:ÄG, b. b. l defin. 6. Men EG är antagen
vara likfor- c’ 11 PTOP- 5-mig med BD; derföre måste
BA:AD==EA:AG;
hvadan . . EA: ÄG = HA:AG, c; hvilket ar omöjligt;
således kan ej diagonalen till BD gå genom K5 eller
någon annan punkt på FG,
På samma sätt bevises, att han ej kan gå genom L,
eller någon annan punkt på EF; alltså måste han gå
genom F, h. s. b.
En parallelogram säges vara applicerad till en gifven
rät linea, så att han brister på en figur, om han ej
upptager hela den gifna lineen.
Parallelogrammen AF är applicerad till AB, och brister
på figuren KM.
<< prev. page << föreg. sida << >> nästa sida >> next page >>