
Full resolution (JPEG) - On this page / på denna sida - Geometry - Problems in geometrical drawings
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
PROBLEMS IN GEOMETRICAL DRAWING. I8 7
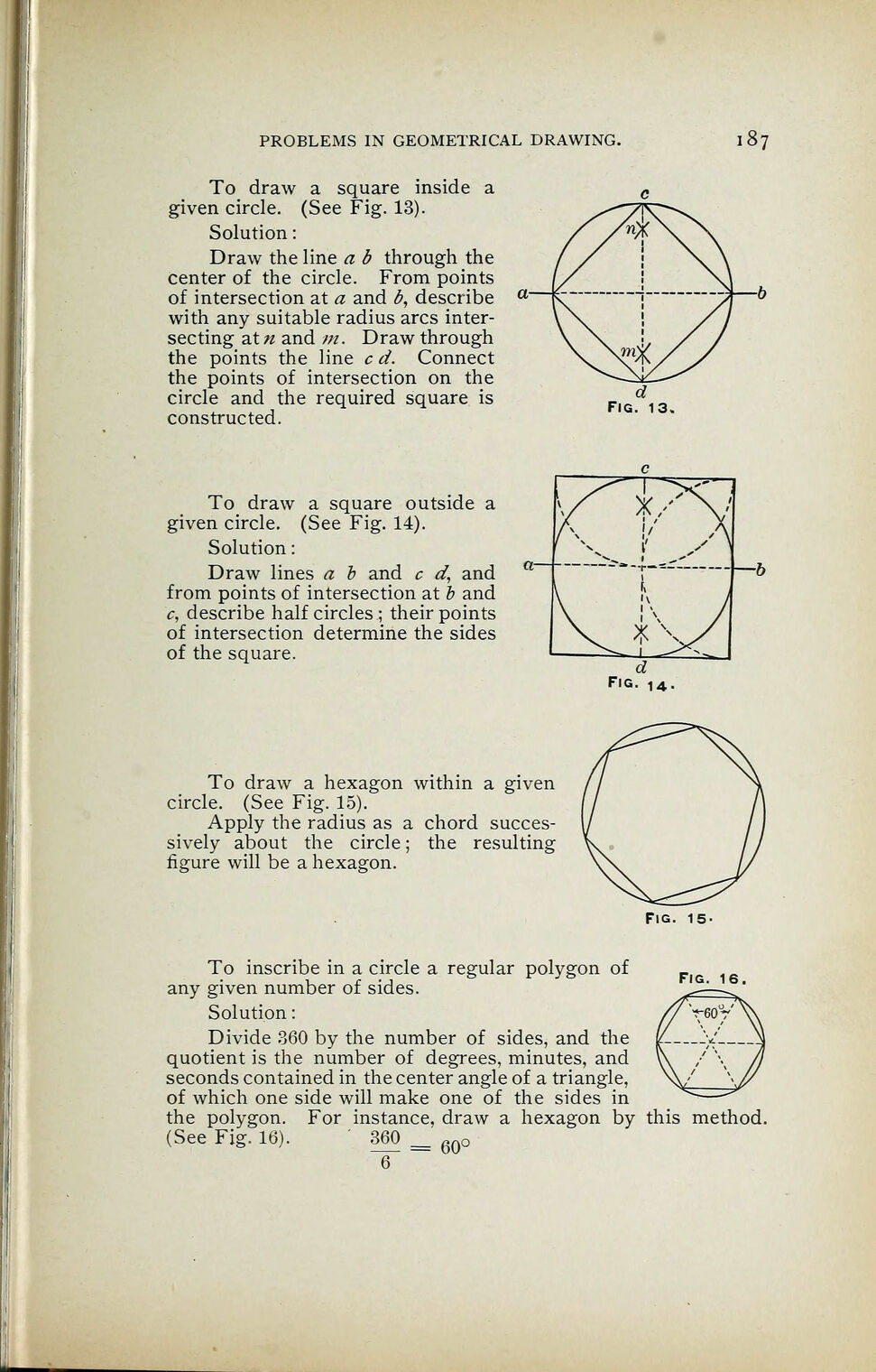
To draw a square inside a
given circle. (See Fig. 13).
Solution
:
Draw the line a b through the
center of the circle. From points
of intersection at a and d, describe
with any suitable radius arcs inter-
secting at n and m. Draw through
the points the line c d. Connect
the points of intersection on the
circle and the required square is
constructed.
To draw a square outside a
given circle. (See Fig. 14).
Solution
:
Draw lines a b and c d, and
from points of intersection at b and
c, describe half circles; their points
of intersection determine the sides
of the square.
To draw a hexagon within a given
circle. (See Fig. 15).
Apply the radius as a chord succes-
sively about the circle ; the resulting
figure will be a hexagon.
Fig. 15-
Fig. 16,
To inscribe in a circle a regular polygon of
any given number of sides.
Solution
:
Divide 360 by the number of sides, and the
quotient is the number of degrees, minutes, and
seconds contained in the center angle of a triangle,
of which one side will make one of the sides in
the polygon. For instance, draw a hexagon by this method.
(See Fig. 16). 360
6
= 60°
<< prev. page << föreg. sida << >> nästa sida >> next page >>