
Full resolution (JPEG) - On this page / på denna sida - Geometry - Problems in geometrical drawings
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
i88 PROBLEMS IN GEOMETRICAL DRAWING.
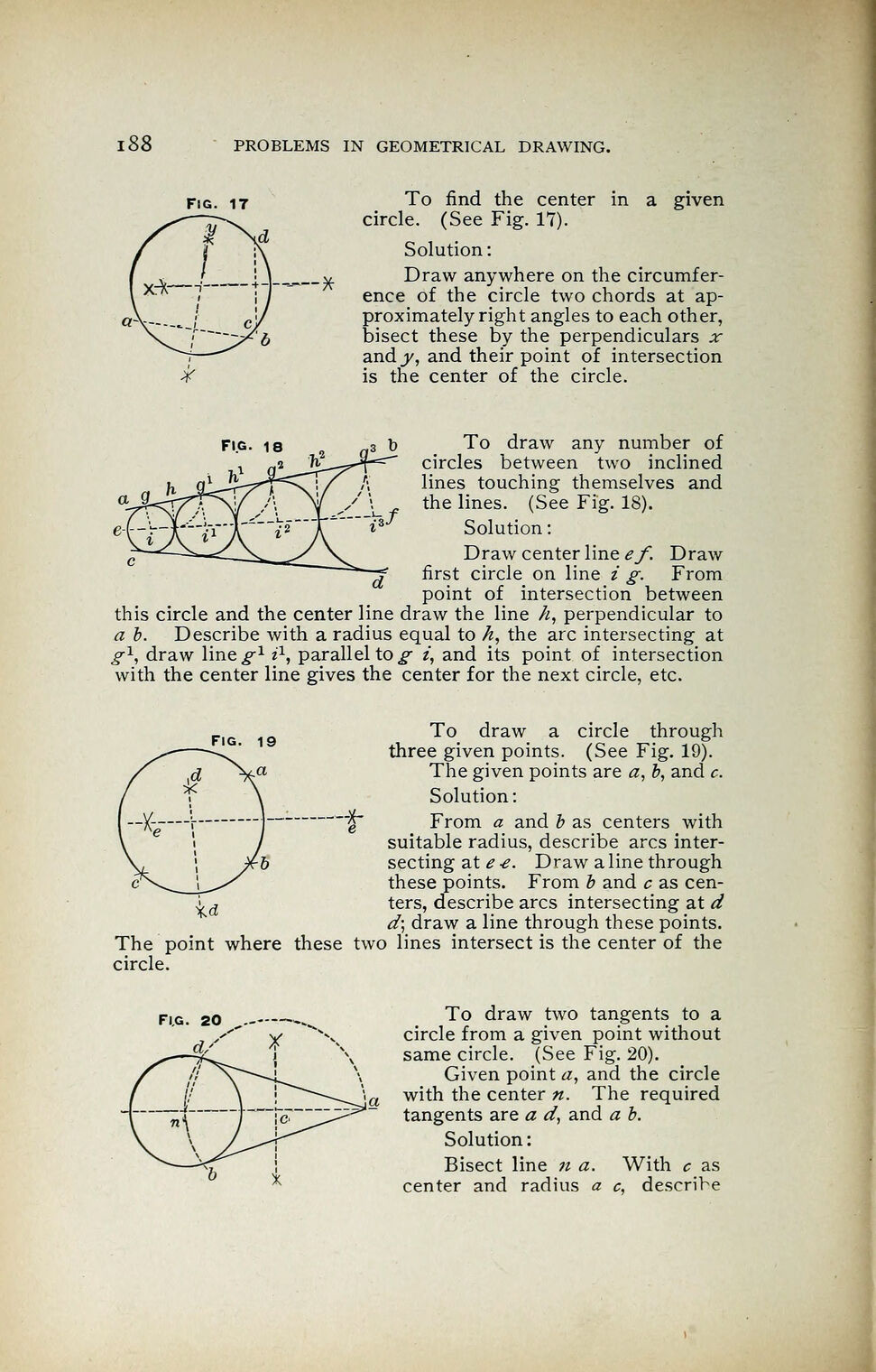
Fig. 17 To find the center in a given
circle. (See Fig. 17).
Solution
:
Draw anywhere on the circumfer-
ence of the circle two chords at ap-
proximately right angles to each other,
bisect these by the perpendiculars x
and y, and their point of intersection
is the center of the circle.
To draw any number of
circles between two inclined
lines touching themselves and
the lines. (See Fig. 18).
Solution
:
Draw center line ef. Draw
first circle on line i g. From
point of intersection between
this circle and the center line draw the line h, perpendicular to
a b. Describe with a radius equal to /i, the arc intersecting at
g1
, draw line^1
i\ parallel to g i, and its point of intersection
with the center line gives the center for the next circle, etc.
Fig.
.. -x-
The point where these
circle.
To draw a circle through
three given points. (See Fig. 19).
The given points are a, b, and c.
Solution:
From a and b as centers with
suitable radius, describe arcs inter-
secting at e -e. Draw a line through
these points. From b and c as cen-
ters, describe arcs intersecting at d
d\ draw a line through these points,
two lines intersect is the center of the
To draw two tangents to a
circle from a given point without
same circle. (See Fig. 20).
Given point #, and the circle
with the center n. The required
tangents are a d, and a b.
Solution
:
Bisect line ;/ a. With c as
center and radius a c, describe
<< prev. page << föreg. sida << >> nästa sida >> next page >>