
Full resolution (JPEG) - On this page / på denna sida - Analysis situs (Topologi) - Analytisk - Analytisk fortsättning - Analytisk geometri
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
897
Analytisk—Analytisk geometri
898
löpa de olika sträckorna hos en geometrisk
figur. Ett annat problem inom a. är det
hittills olösta s. k. kartfärgsproblemet.
Det är en känd sak bland kartritare, att det
fordras minst fyra olika färger för att vid
färgläggning av en karta, där ländernas antal
och läge äro godtyckliga, undvika, att två
lika färger gränsa intill varandra. Beviset
för att det också är tillräckligt med fyra
färger saknas ännu. Inom a. behandlas
ofta frågor, som röra olika kurvor, som äro
slingrade in i varandra, t. ex. de »borromeiska
ringarna» (se fig. 2), som äro inkedjade i
varandra på så sätt, att om man tar bort en av
dem, vilken som helst, så falla de båda
återstående isär. T. B.
Analytisk, upplösande, sönderdelande,
utredande.
Analytisk fortsättning, ett begrepp i
funk-tionsteorien (se d. o.).
Analytisk geometri, egentligen den del av
matematiken, som utgör analysens (se
d. o.) tillämpningar i geometrien och för
vilken det följaktligen är vanskligt att
utstaka några bestämda gränser. Enligt svenskt
språkbruk menar man med a.
huvudsakligen den gren av geometrien, som begagna”
sig av algebran som hjälpmedel vid
undersökningen av linjers och ytors egenskaper.
En nödvändig förutsättning härför blir
följaktligen, att de geometriska storheterna
(linjer, ytor, vinklar etc.) uttryckas i tal genom
deras jämförelse med ett gemensamt mått.
Sedan man uttryckt de geometriska
storheterna i tal, kan man åvägabringa ekvationer,
som avspegla egenskaperna hos olika figurer.
Den analytiska geometrien indelas i p 1 a
n-och rymdgeometri; den förra sysslar
huvudsakligen med de s. k. k o n i s k a
sektionerna (se d. o.) eller k ä g e 1 s n i
t-t e n och några kurvor av högre ordning,
medan rymdgeometrien behandlar räta linjer i
rymden och sådana ytor, som kunna uttryckas
i ekvationer av l:a eller 2:a graden.
Grundvalen för studiet av den analytiska
geometrien är införandet av ett fast
koordinatsystem (se d. o.), till vilket varje
punkt i planet kan hänföras genom enkla
relationer. Inför man sålunda i den plana
analytiska geometrien det rätvinkliga
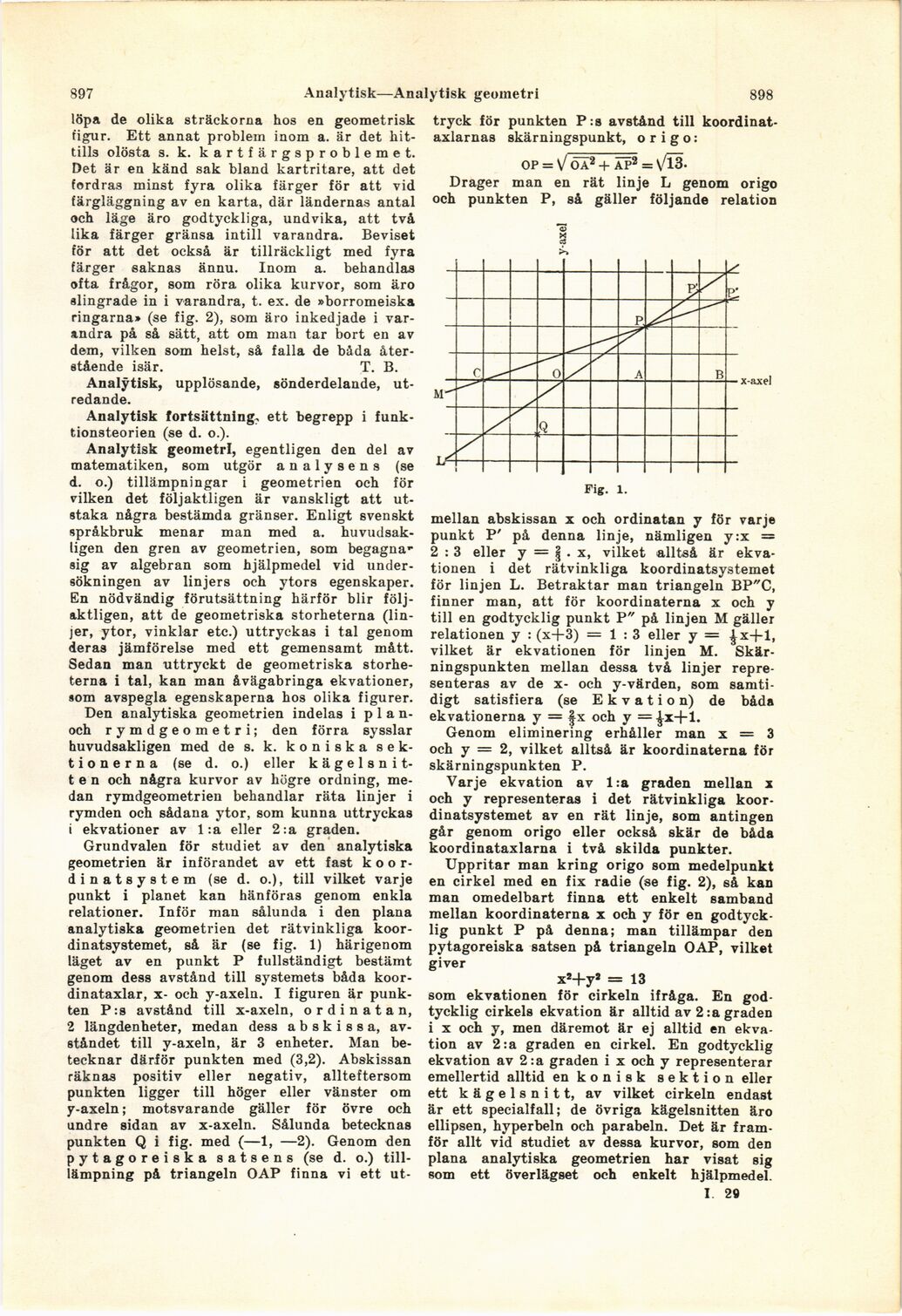
koordinatsystemet, så är (se fig. 1) härigenom
läget av en punkt P fullständigt bestämt
genom dess avstånd till systemets båda
koor-dinataxlar, x- och y-axeln. I figuren är
punkten P :s avstånd till x-axeln, ordinatan,
2 längdenheter, medan dess abskissa,
avståndet till y-axeln, är 3 enheter. Man
betecknar därför punkten med (3,2). Abskissan
räknas positiv eller negativ, allteftersom
punkten ligger till höger eller vänster om
y-axeln; motsvarande gäller för övre och
undre sidan av x-axeln. Sålunda betecknas
punkten Q i fig. med (—1, —2). Genom den
pytagoreiska satsens (se d. o.)
till-lämpning på triangeln OAP finna vi ett ut-
tryck för punkten P:s avstånd till
koordinat-axlarnas skärningspunkt, o r i g o:
OP = V ÖÄ2 + ÄP2 = \z13.
Drager man en rät linje L genom origo
och punkten P, så gäller följande relation
mellan abskissan x och ordinatan y för varje
punkt P’ på denna linje, nämligen y:x =
2 : 3 eller y = | . x, vilket alltså är
ekvationen i det rätvinkliga koordinatsystemet
för linjen L. Betraktar man triangeln BP"C,
finner man, att för koordinaterna x och y
till en godtycklig punkt P" på linjen M gäller
relationen y : (x+3) = 1:3 eller y = ^x-|-l,
vilket är ekvationen för linjen M.
Skärningspunkten mellan dessa två linjer
representeras av de x- och y-värden, som
samtidigt satisfiera (se Ekvation) de båda
ekvationerna y = |x och y =|x+l.
Genom eliminering erhåller man x = 3
och y = 2, vilket alltså är koordinaterna för
skärningspunkten P.
Varje ekvation av l:a graden mellan x
och y representeras i det rätvinkliga
koordinatsystemet av en rät linje, som antingen
går genom origo eller också skär de båda
koordinataxlarna i två skilda punkter.
Uppritar man kring origo som medelpunkt
en cirkel med en fix radie (se fig. 2), så kan
man omedelbart finna ett enkelt samband
mellan koordinaterna x och y för en
godtycklig punkt P på denna; man tillämpar den
pytagoreiska satsen på triangeln OAP, vilket
giver
X2+ys = 13
som ekvationen för cirkeln ifråga. En
godtycklig cirkels ekvation är alltid av 2 :a graden
i x och y, men däremot är ej alltid en
ekvation av 2:a graden en cirkel. En godtycklig
ekvation av2:a graden i x och y representerar
emellertid alltid enkonisk sektion eller
ett k ä g e 1 s n i 11, av vilket cirkeln endast
är ett specialfall; de övriga kägelsnitten äro
ellipsen, hyperbeln och parabeln. Det är
framför allt vid studiet av dessa kurvor, som den
plana analytiska geometrien har visat sig
som ett överlägset och enkelt hjälpmedel.
I 29
Fig. 1.
<< prev. page << föreg. sida << >> nästa sida >> next page >>