
Full resolution (JPEG) - On this page / på denna sida - Vågrörelse
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
819
Vågrörelse
820
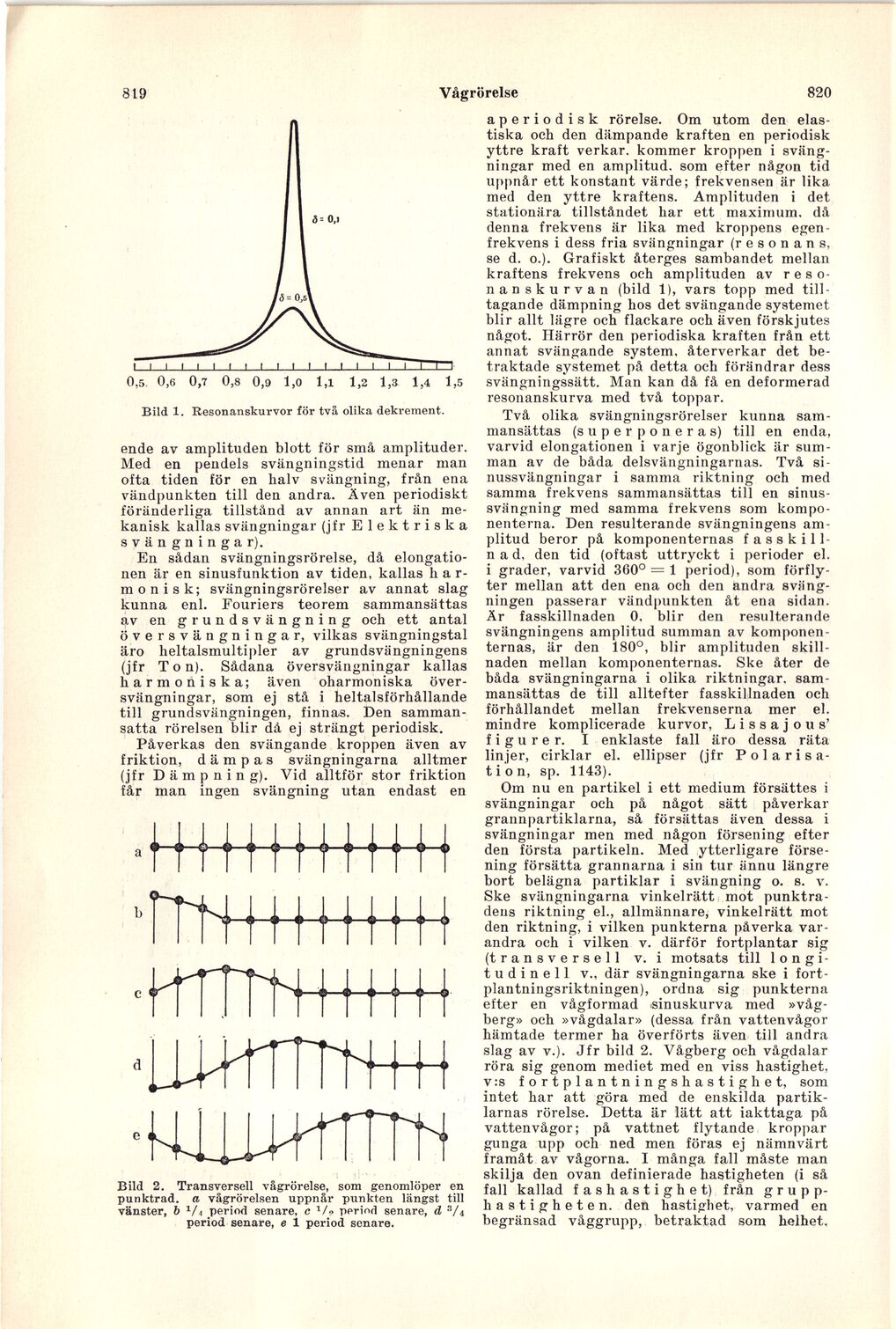
Bild 1. Resonanskurvor för två olika dekrement.
ende av amplituden blott för små amplituder.
Med en pendels svängningstid menar man
ofta tiden för en halv svängning, från ena
vändpunkten till den andra. Även periodiskt
föränderliga tillstånd av annan art än
mekanisk kallas svängningar (jfr Elektriska
svängningar).
En sådan svängningsrörelse, då
elongatio-nen är en sinusfunktion av tiden, kallas h a
r-monisk; svängningsrörelser av annat slag
kunna enl. Fouriers teorem sammansättas
av en grundsvängning och ett antal
översvängningar, vilkas svängningstal
äro heltalsmultipler av grundsvängningens
(jfr Ton). Sådana översvängningar kallas
harmoniska; även oharmoniska
översvängningar, som ej stå i heltalsförhållande
till grundsvängningen, finnas. Den
sammansatta rörelsen blir då ej strängt periodisk.
Påverkas den svängande kroppen även av
friktion, dämpas svängningarna alltmer
(jfr Dämpning). Vid alltför stor friktion
får man ingen svängning utan endast en
Bild 2. Transversell vågrörelse, som genomlöper en
punktrad. a vågrörelsen uppnår punkten längst till
vänster, b 4 period senare, c x/-> period senare, d 3/<
period senare, e 1 period senare.
aperiodisk rörelse. Om utom den
elastiska och den dämpande kraften en periodisk
yttre kraft verkar, kommer kroppen i
svängningar med en amplitud. som efter någon tid
uppnår ett konstant värde; frekvensen är lika
med den yttre kraftens. Amplituden i det
stationära tillståndet har ett maximum, då
denna frekvens är lika med kroppens
egenfrekvens i dess fria svängningar (resonans,
se d. o.). Grafiskt återges sambandet mellan
kraftens frekvens och amplituden av
resonanskurvan (bild 1), vars topp med
tilltagande dämpning hos det svängande systemet
blir allt lägre och flackare och även förskjutes
något. Härrör den periodiska kraften från ett
annat svängande system, återverkar det
betraktade systemet på detta och förändrar dess
svängningssätt. Man kan då få en deformerad
resonanskurva med två toppar.
Två olika svängningsrörelser kunna
sammansättas (superponeras) till en enda,
varvid elongationen i varje ögonblick är
summan av de båda delsvängningarnas. Två
si-nussvängningar i samma riktning och med
samma frekvens sammansättas till en
sinus-svängning med samma frekvens som
komponenterna. Den resulterande svängningens
amplitud beror på komponenternas f a s s k i
11-n a d, den tid (oftast uttryckt i perioder el.
i grader, varvid 360° = 1 period), som
förflyter mellan att den ena och den andra
svängningen passerar vändpunkten åt ena sidan.
Är fasskillnaden 0, blir den resulterande
svängningens amplitud summan av
komponenternas, är den 180°, blir amplituden
skillnaden mellan komponenternas. Ske åter de
båda svängningarna i olika riktningar,
sammansättas de till alltefter fasskillnaden och
förhållandet mellan frekvenserna mer el.
mindre komplicerade kurvor, Lissajous’
figurer. I enklaste fall äro dessa räta
linjer, cirklar el. ellipser (jfr
Polarisation, sp. 1143).
Om nu en partikel i ett medium försättes i
svängningar och på något sätt påverkar
grannpartiklarna, så försättas även dessa i
svängningar men med någon försening efter
den första partikeln. Med ytterligare
försening försätta grannarna i sin tur ännu längre
bort belägna partiklar i svängning o. s. v.
Ske svängningarna vinkelrätt mot
punktradens riktning el., allmännare, vinkelrätt mot
den riktning, i vilken punkterna påverka
varandra och i vilken v. därför fortplantar sig
(transversell v. i motsats till
longitudinell v., där svängningarna ske i
fort-plantningsriktningen), ordna sig punkterna
efter en vågformad sinuskurva med
»vågberg» och »vågdalar» (dessa från vattenvågor
hämtade termer ha överförts även till andra
slag av v.). Jfr bild 2. Vågberg och vågdalar
röra sig genom mediet med en viss hastighet,
v :s fortplantnings hastig het, som
intet har att göra med de enskilda
partiklarnas rörelse. Detta är lätt att iakttaga på
vattenvågor; på vattnet flytande kroppar
gunga upp och ned men föras ej nämnvärt
framåt av vågorna. I många fall måste man
skilja den ovan definierade hastigheten (i så
fall kallad fashastighet) från
grupphastigheten. den hastighet, varmed en
begränsad våggrupp, betraktad som helhet.
<< prev. page << föreg. sida << >> nästa sida >> next page >>