Salmonsens konversationsleksikon / Anden Udgave / Bind X: Gradischa—Hasselgren / 498 (1915-1930) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Gyroskop - Gyroskopbaner - Gyroskop-Kollimator - Gyrostat - Gyrotrop - Gyrovager - Gyrowetz, Adalbert

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

forstaaeligere. Fig. 1 forestiller en Top, der
snurrer om sin Akse i den Retning, der
angives ved Pilen a. Ovenfra ses Bevægelsen at
gaa med Urviseren. Vi antager først, at
Toppens Akse er spids forneden, og at den kan
bore sig lidt ned i Underlaget, saa den hindres
i at glide paa dette. Begynder man med at
støtte Aksen i dens afbildede skraa Stilling og
derpaa pludselig slipper den, saa vil den vel
straks begynde at falde, men herved kommer
Kraften (Toppens Vægt) til at dreje den om en
Linie, der gaar gennem Spidsen og staar
vinkelret paa Figurens Plan. Set forfra gaar denne
Drejning ogsaa med Urviseren. Følgelig skal
Toppens Akse begynde at bevæge sig
fremefter, men den naar aldrig at falde sammen
med den vandrette Omdrejningsakse gennem
Spidsen: thi denne staar altid vinkelret paa
den lodrette Plan gennem Toppens Akse og
viger følgelig bort. Resultatet bliver, at Toppens
Akse kommer til at løbe rundt om Vertikalen
gennem Spidsen i den Retning, som Pilen b
viser. Aksen udfører herved en
»Præeessionsbevægelse«, der er desto langsommere, jo
hurtigere Toppen snurrer rundt, jo nærmere dens
Tyngdepunkt ligger ved Spidsen, og jo længere
dens Masse er fjernet fra Aksen. Blandet med
Præcessionen er, især i Beg., en »Nutation«,
der bestaar i smaa Fald og Stigninger af Aksen.
— Er det vandrette Underlag haardt og saa
glat, at Spidsen kan glide paa det uden
kendelig Modstand, bliver Bevægelsen særlig elegant.
Har Toppens Tyngdepunkt fra først af ingen
Bevægelse i vandret Retning, vil det heller
ikke faa nogen, og det indskrænker sig til at
gøre smaa Bevægelser op og ned, alt efter som
Aksen snart rejser sig mere op, snart falder
noget. Spidsen løber rundt paa Underlaget og
holder sig under sin Bevægelse mellem to
Cirkler, hvis fælles Centrum ligger under Toppens
Tyngdepunkt. Mellem disse Cirkler tegner den
Buer, hvis Hulning vender indad, og som
støder sammen i Spidser paa den indre Cirkels
Omkreds. — Fig. 2 forestiller
Bohnenberger’s Rotationsapparat (1810), der er det første
egl. G. En Kugle roterer om en Akse, der er
Diameter i en Cirkelring; denne Ring kan atter
ved Hjælp af et Par Spidser dreje sig om en
paa den første vinkelret Diameter, der tillige
er Diameter i en anden Ring, som endelig
atter er drejelig om en Diameter, der staar
vinkelret paa den sidst nævnte. Kuglens Akse
har da Frihed til at stille sig i en hvilken som
helst Retning, og Apparatet tjener til at vise de
Bevægelser, som Aksen vil udføre, naar man
ved Slag, paahængte Vægte ell. andre Midler
søger at forandre dens Retning. Fastgør man
den lodrette Akse, tager Apparatet i Haanden
og fører det rundt i en vandret Kreds, vil den
roterende Kugles Akse stille sig lodret. Navnet
G. er indført af Foucault, der gav det til
et Instrument, som han konstruerede 1852, og
ved hvis Hjælp han kunde paavise Jordens
Rotation. Med større ell. mindre Held har man
til forsk. Tider søgt at bringe et G. i
Forbindelse med Sekstanten for om Bord paa Skibe
at kunne maale Himmellegemers Højde, naar
Horisonten ikke er synlig. Skibets Bevægelse
forhindrer nemlig Anvendelsen af Lodsnor ell.
Kvægsølvhorisont, medens det langt stabilere
G. kan bruges. Selve Jorden er et
kæmpemæssigt G. Jordaksen danner en Vinkel paa 23 1/2°
med Normalen til Ekliptikas Plan; p. Gr. a.
Jordens Fladtrykning søger Solen at stille
Jordaksen vinkelret paa denne Plan; men Følgen
bliver kun, at Aksen kommer til i Løbet af
henimod 26000 Aar at beskrive en Kegleflade
omkring Planens Normal som geometrisk Akse
(Præcession). Den mat. Behandling af G.
kan ikke gives her, men maa søges i de
udførligere Lærebøger i rationel Mekanik. En
populær Fremstilling findes i John Perry’s
Spinning Tops (London 1890). Om G.’s Anvendelse
til Erstatning for Magnetnaalen i
Skibskompasset, se Kompas.
<i>K. S. K./i>

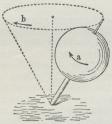Fig. 1.

Fig. 2.

Gyroskopbaner, se Enskinnebaner.

Gyroskop-Kollimator (Søv.), et Instrument
konstrueret af en fr. Søofficer, Fleuriais,
der i Skibe benyttes ved Maaling af
Himmellegemers Højde, naar Kimmingen ikke er
synlig. Apparatet støtter sig til det ovf. i
Gyroskop nævnte Princip. Ved Rotationen af 2
Glaslinser, der hver er forsynede med en sort
Streg, danner de to Streger en ubrudt Linie,
der træder i St. for hvad man ved Maalinger
i Land kalder kunstig Horisont, og til hvilken
der maales med en alm. Sekstant, paa hvilken
G. er anbragt.
H. E.

Gyrostat (gr.) en Art Gyroskop opfundet
og anvendt til Undervisningsbrug af William
Thomson.

Gyrotrop, se Strømvender.

Gyrovager (gr.-lat.: »Landstrygere«), Munke,
som uden noget fast Opholdssted strejfede om
fra Kloster til Kloster. Da Benedikt fra Nurcia’s
Regel, hvori stabilitas loci (fast Opholdssted)
var en af Hovedgrundsætningerne, blev
eneherskende i den vesterlandske Kirke, forsvandt G.
L. M.

Gyrowetz [’giråvæts], Adalbert, bøhmisk
Komponist, (1763—1850), kom efter et noget
omflakkende Ungdomsliv til Wien, hvor han 1804
blev Dirigent ved Hofoperaen. Denne Stilling
beklædte han til 1831 og nød i denne Periode
høj Anseelse som Komponist af utallige
Symfonier, Operaer, Strygekvartetter, Ouverturer,
Serenader o. s. v., men overlevede rigtignok
længe sit Ry. G. hørte til de Musikere, der
uden Oprindelighed, men med en vis naturlig
Musikbegavelse sluttede sig nær til Haydn og
Mozart, og som af Samtiden noget nær sattes
jævnsides disse to Mestre. G. har efterladt sig
en interessant Selvbiografi (1848).
W. B.

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>