
Full resolution (TIFF) - On this page / på denna sida - Kooptation - Koordinater

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
været hjemlet. Saaledes sad der i det fr. Senat
efter Loven af 24. Febr 1875 foruden 225
Medlemmer, valgte af Departementerne, 75 valgte
for Livstid af Nationalforsamlingen, og naar
nogen af de sidste afgik, skulde Senatet selv
besætte den ledige Plads, jfr. Lovens Art. 7.
Denne Ordning afskaffedes dog 1884. I
Danmark derimod gælder endnu den ved Grl. af 5.
Juni 1915 § 36 indførte Regel, hvorefter 1/4 af
Landstingets Medlemmer vælges af det
afgaaende Landsting selv, hver Gang Landstinget
opløses ell. de landstingsvalgte Medlemmers
8-aarige Periode er udløbet — en Regel,
hvormed man har villet styrke Kontinuiteten i
Landstinget.
K. B.
Koordinater (lat.) (mat.). I Geometrien
angiver man ofte Beliggenheden af et Punkt, en
Linie, en Plan ell. almindeligere en Figur af en
bestemt Art ved Tal, som udtrykker Egenskaber ved
Figurens Beliggenhed i Forhold til en fast
Figur; disse Tal kaldes K., og den faste Figur
taldes Koordinatsystemet. Ved disse
Bestemmelser ved K. regnes Længder paa
Linier alm. med Fortegn (se Geometri), og
Liniers Vinkler med en fast Linie ell. Punkters
Afstande fra en saadan Linie regnes positive
til den ene, negative til den anden Side af
Linien. Beliggenheden af et Punkt paa en
given ret Linie kan udtrykkes ved en enkelt K.,
Punktets Abscisse ɔ: det Tal, som i en vis
Længdeenhed udtrykker Afstanden fra et fast
Begyndelsespunkt paa Linien til Punktet; som
K. kam ogsaa bruges det Forhold, hvori Punktet
deler Stykket mellem to givne Punkter paa
Linien, ell. dets Dobbeltforhold (s. d.) med tre
givne Punkter paa linien. Som K. for Linier
i en Plan gennem et fast Punkt (Liniebundt)
ell. for Planer gennem en fast ret Linie
(Planbundt) bruges alm. tg til Vinklen med en fast
til Bundtet hørende Linie ell. Plan. Et Punkt
paa en given Kurve bestemmes ogsaa hyppig
ved en enkelt K., paa et Keglesnit f. Eks. ved
K. til en Linie gennem Punktet, hørende til
Liniebundtet gennem et fast Punkt paa
Keglesnittet. I Descartes’ analytiske Geometri
bestemmes et Punkt i en Plan ved
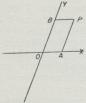
Parallelkoordinater. Koordinatsystemet (Fig. 1)
bestaar af to rette Linier, Koordinatakserne,
nemlig Abscisseaksen x og
Ordinataksen y, der skærer hinanden i
Begyndelsespunktet O, og K. til et Punkt P
er de Stykker OA, Abscissen, og OB,
Ordinaten, som Paralleller med Akserne
gennem P afskærer. Koordinatsystemet kaldes
retvinklet, hvis Akserne er vinkelrette paa
hinanden, ellers skævvinklet. Paa lgn. Maade
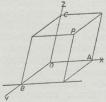
kan man i Rummet som Koordinatsystem
bruge tre rette Linier, X, Y, Z, gennem samme
Punkt (Fig. 2), og som et Punkt P’s K. de
Stykker, OA, OB og OC, som afskæres paa en
Akse af en Plan gennem P parallel med de to
andre Akser. Staar Akserne parvis vinkelrette
paa hinanden, kaldes Koordinatsystemet
treretvinklet. De saakaldte
Trekantskoordinater ell. trilineære K. er
først benyttede af Möbius og Plücker. De
kaldes Punktkoordinater eller
Liniekoordinater, efter som de anvendes til
Bestemmelse af Punkter ell. Linier i en Plan.
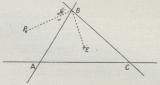
I første Tilfælde (Fig. 3) bestaar
Koordinalsystemet af en Trekant ABC og et uden for
dennes Sider valgt Punkt E, Enhedspunktet.
Et Punkt P’s K. er dets Afstande fra
Koordinattrekantens Sider dividerede med
Enhedspunktets Afstande fra de samme Sider; to K.’s
Forhold er et Dobbeltforhold som det mellem
Linierne BA, BC, BE, BP. Ved
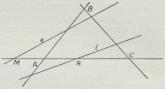
Liniekoordinater (Fig. 4) bestaar Koordinatsystemet af en
Trekant ABC og en Enhedslinie e. En
Linie l’s K. er dens Afstande fra
Koordinattrekantens Vinkelspidser dividerede med
Enhedsliniens Afstande fra de samme Vinkelspidser;
to K.’s Forhold er et Dobbeltforhold som
(ACMR). To Figurer, hvis Punkter (ell. Linier)
bestemmes ved de samme K. i to forsk.
Trekantskoordinatsystemer, er hinandens
Centralprojektioner; er en Sætning om en Figur bevist
ved Hjælp af et Trekantskoordinatsystem, gælder
den om alle Centralprojektioner af Fig. Tillige
vil to Figurer, der i et
Trekantspunktkoordinatsystem og et Trekantsliniekoordinatsystem
bestemmes ved de samme K., svare dualistisk
til hinanden (se Dualitet), og man kan
altsaa ved de samme
Regninger bevise en
Sætning og den dualistisk
tilsvarende. Paa
ganske lgn. Maade
bruger man i Rummet et
Tetraeder som
Koordinatsystem baade for
Punktkoordinater og
for Plankoordinater. Et andet meget
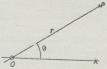
benyttet Slags K. er Polarkoordinater.
Her bestaar Koordinatsystemet i Planen (Fig.
5) af en fast ret Linie X og et fast Punkt O,
 |
| Fig. 1. |
 |
| Fig. 2. |
 |
| Fig. 3. |
 |
| Fig. 4. |
 |
| Fig. 5. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>