
Full resolution (TIFF) - On this page / på denna sida - Kvadrant (astronomisk Instrument) - Kvadrant (Instrument) - Kvadrantjern - Kvadrat (mat.) - Kvadrat (mus.) - Kvadrat (i typografi) - Kvadratalen - kvadratisk - kvadratisk Form - kvadratisk Ligning - Kvadratjern - Kvadratmaal - Kvadratrix

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Kvadrant kaldtes hos de ældre Astronomer
et Instrument til at maale en Stjernes Højde.
Da man havde Vanskelighed med at forfærdige
og dele nøjagtig større Helcirkler, nøjedes man
med Fjerdeparten af denne, K., og disse var
dels transportable, dels fast opstillede. Ved de
transportable var Gradbuen befæstet til en
vertikal Søjle, saa at een Radius stod vertikal og
een horisontal. Om K.’s Centrum drejede sig
et Sigteapparat (i den ældste Tid et Diopter,
senere en Kikkert) med Alhidade. De fast
opstillede K. benyttedes til nøjagtigere
Observationer, og alm. var de befæstede til en vertikal
Murvæg, som var orienteret ret N.—S.; derfor
kaldes disse K. alm. Murkvadranter.
Med disse maaltes Stjernens Højde i
Meridianen, og med Kendskab til Stedets Bredde havde
man Stjernens Deklination. I Østen blev de
første K. konstruerede af Araberne, i Europa af
Tyge Brahe 1587, der har beskrevet sin
Quadrans muralis sive Tichonicus. Af mere
bekendte Murkvadranter kan nævnes den, som
Bradley benyttede i Greenwich og Lalande i
Paris, begge var forfærdigede af Bird. Nu har
Meridiancirkelen fortrængt Murkvadranten.
J. Fr. S.
Kvadrant, et Instrument, der anvendes til
at bestemme Elevationen ved svært Skyts. K.,
der sædvanlig er af Messing, bestaar
almindeligst af 2 Linealer, der støder sammen under
en ret Vinkel, og hvis Ender er forbundne med
en i Grader og Minutter inddelt Cirkelbue, der
har sit Centrum i Linealernes
Sammenstødspunkt. Om dette samme Punkt drejer sig en
bevægelig Viser, der peger paa den inddelte
Cirkelbue og oftest i Enden er forsynet med en
Nonius, ved Hjælp af hvilken man saaledes
kan aflæse den Vinkel, Viseren danner med
den ene Lineal. Viseren bærer paa Midten en
Rørlibelle. Stiller man altsaa Viseren, saa den
danner en bestemt Vinkel med den ene Lineal,
og anbringer man dernæst K. paa en med
Kernelinien parallel Flade — Kvadrantfladen
— paa Kanonen, vil dennes Kernelinie, naar
Kanonen drejes saa meget om sine Tappe, at
Libellen »spiller ind«, danne samme Vinkel
med Horisontalplanet, som Viseren dannede
med Linealen. Har man omvendt givet Kanonen
en vis Elevation — bragt dens Kernelinie til at
danne en vis Vinkel med Horisontalplanet —
kan man ved at stille K. paa Kvadrantfladen
og bevæge Viseren, til Libellen »spiller ind«,
aflæse, hvor stor denne Vinkel er.
H. H.
Kvadrantjern, Profiljern, hvis Tværsnit
danner en Kvartcirkel begrænset af to
udadvendende radiære Flige, har været brugt til
Søjler, idet de nittedes sammen 4 og 4.
E. Su.
Kvadrat (mat.) kaldes en Firkant, hvis Sider
er lige store, og hvis Vinkler alle er rette. K.’s
Fladeindhold maales ved anden Potens af dets
Side, ɔ: anden Potens af Antallet af
Længdeenheder i K.’s Side er = Antallet af
tilsvarende kvadratiske Fladeenheder i K.; derfor
kaldes anden Potens af en Størrelse hyppigt
dens K.
Chr. C.
Kvadrat (mus.) (fr. bécarre, eng. natural),
Opløsningstegn, Tegnet ♮), der, sat foran en
Node, ophæver et foregaaende ♯ ell. ♭.
Kvadrat (tysk: Konkordanz, eng.: 4 m-quad,
fr.: cadrat sur quatre douzes) kaldes i
Typografien den bredeste Udslutning til det tomme
Rums Udfyldning i Udgangslinier. En K. er
dog ikke, som Navnet antyder, et Typelegeme
med kvadratisk Tværsnit, idet Højde og Bredde
er noget forsk. En fr. K. er 4 1/4 Cicero fr. høj
= 19,17 mm, Bredden derimod 4 Cicero fr. =
18,046 mm. En tysk K. er 4 1/2 Cicero tysk høj
= 19,46 mm, Bredden 4 Cicero tysk = 17,28
mm. Der findes ogsaa halve K. = 2 Cicero, 3/4
K. = 3 Cicero.
E. S-r.
Kvadratalen, se Flademaal.
kvadratisk (mat.), formet som et Kvadrat.
Et Polynomium ell. en Ligning af 2. Grad
kaldes k. (se Kvadrat).
Chr. C.
kvadratisk Form (mat.), d. s. s. et
Polynomium af 2. Grad m. H. t. visse Bogstaver.
De m. H. t. to Bogstaver homogene k. F.
spiller en betydelig Rolle i Talteorien; de er
undersøgte af Gauss, Lejeune-Dirichlet og andre.
Chr. C.
kvadratisk Ligning (mat.), d. s. s. Ligning
af 2. Grad. Se Ligninger.
Kvadratjern, Stangjern med kvadratisk
Tværsnit.
E. Su.
Kvadratmaal, se Flademaal.
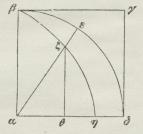
Kvadratrix (mat.) er en Kurve (paa Fig.
βζη), der beskrives af et Punkt ζ bestemt paa
flg. Maade: Der er
givet en
Cirkelkvadrant αβεδ; er
αε Radien i denne
gennem ζ, skal ζ’s
Afstand ζθ fra
Radien αδ forholde
sig til αβ som Buen
εδ til
Cirkelkvadrantens Bue βδ.
K. skal oprindelig
være udtænkt af
Hippias til Brug
ved Vinkelens Tredeling; da < δαε er
proportional med ζθ, vil Punktet ζ svarende til en
Vinkel = 1/3. < δαε have Afstanden 1/3. δθ fra
αδ og følgelig let kunne konstrueres, naar K.
er tegnet. Navnet K. skyldes Kurvens
Anvendelighed til Cirkelens Kvadratur, hvilken først er
paavist af Deinostratos; da ∩βδ/αβ = εδ/ζθ, og
dette sidste Forhold kan vises at blive = αδ/αη,
naar ε falder i δ, faas Cirkelens Areal = 4·1/2.
αδ·∩βδ = αδ· αδ2/η. hvor αδ2/η kan konstrueres
som Fjerdeproportional til bekendte
Liniestykker, naar K. er tegnet.
Chr. C.
 |
<< prev. page << föreg. sida << >> nästa sida >> next page >>