Salmonsens konversationsleksikon / Anden Udgave / Bind XV: Kvadratrod—Ludmila / 115 (1915-1930) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Kædebrøk - Kædegarn - Kædehandel - Kædehjul - Kædeled - Kædelinie - Kæden - Kædenitning ell. Siksaknitning - Kædeordenen

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

fuldstændige Kvotient x₁ er > 1; a₁ er det hele Tal
nærmest lavere end x₁ o. s. v. En Brøk giver
ved Udvikling en K. med et endeligt Antal
ufuldstændige Kvotienter, og en saadan K. er
altid Udtryk for en Brøk; en positiv irrational
Rod i en kvadratisk Ligning med rationale
Koefficienter giver en i det uendelige fortsat K.,
der fra et vist Punkt at regne bestaar af den
samme Række ufuldstændige Kvotienter
gentaget i det uendelige, og omvendt er en
saadan periodisk K. altid Rod i en
kvadratisk Ligning med rationale Koefficienter. Den
første Del af K. op til a, f. Eks. a_r
inklusive, kaldes en Konvergent og betegnes
ved y_r/z_r, hvor med y_r og z_r menes Tæller og
Nævner i den nævnte Del af K.
skrevet som uforkortelig Brøk. Til successiv
Beregning af Konvergenterne tjener Formlen:
y_r/z_r = y_r÷1a_r+y_r—2 / z_r—1a_r+z_r—2. Konvergenterne er
Tilnærmelsesværdier til K., stadig bedre, jo større
r bliver, og mindre ell. større end K., efter
som r er lige ell. ulige; y_r/z_r’s Afvigelse fra K.
er mindre end 1/z_r². Sætter man i St. f. en
Konvergent en anden Tilnærmelsesværdi paa
Brøks Form, faar man enten en større Nævner
ell. en daarligere Tilnærmelse. Denne Maade
at danne Tilnærmelsesværdier paa
anvendes f. Eks. til tilnærmet Beregning af Rødder
i Ligninger ell. til at erstatte Brøker ved andre
med mindre Tæller og Nævner. Vil man
saaledes udtrykke Forholdet mellem en fr. og en
eng. Fod, der meget nær er = 3600/3379, ved
simplere Tal, udvikles i K., hvorved faas de
ufuldstændige Kvotienter 1, 15, 3, 2, 4, 1, 5 og
Konvergenterne 1/1, 16/15, 49/46,114/107,505/474,619/581,3600/3379. Man
har da f. Eks.: 1/ fr. Fod/1 eng. Fod — 505/474 < 1/474², ell.
474 fr. Fod — 505 eng. Fod < 1 eng. Fod/474, ɔ:
sætter man 474 fr. Fod = 505 eng. Fod, er den
begaaede Fejl < 1/474 af en eng. Fod. Andre
vigtige Anvendelser af K. forekommer ved
Løsningen af ubestemte Ligninger (s. d.) og i
Talteorien. Man har ogsaa behandlet mere alm.
Former for K., hvor der i St f. Ettallene og
a’erne staar vilkaarlige Tal, og har der fundet
en lgn. simpel Metode til successiv Beregning
af Konvergenterne som ovf. samt
Konvergensbetingelser for uendelige K.
Chr. C.

Kædegarn, se Vævning.

Kædehandel. Herved forstaas en
fordyrende, uproduktiv Varehandel, hvorved Varen gaar
fra Haand til Haand i samme Omsætningsled
ell. maaske endog tilbage f. Eks. fra Detaillist
til Grossist, ell. hvor der indskydes helt nye,
ellers udenforstaaende Mellemhandlere som
Mellemled i Varens (normale) Omsætning.
Ch. V. N.

Kædehjul, Tandhjul, hvis Tænder griber ind
i Ledene paa en Kæde, saa at enten Hjulet tager
Kæden med sig, naar det drejes, ell. Kæden
tager Hjulet med, sig, naar der trækkes i den.
Nærliggende Eksempler paa K. frembyder
simplere Væggeure, hvis Lodder hænger i Kæder,
og Cykler.
F. W.

Kædeled, den enkelte Del, hvoraf en Kæde
bestaar.

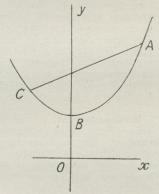
Kædelinie (mat.) kaldes den Kurve (paa
Fig. CBA), der dannes af en i to Punkter (A
og C) ophængt uelastisk Snor, forudsat at
Vægtene af vilkaarlige Stykker af Snoren er
proportionale med Stykkernes Længder. K., der
først er undersøgt af Joh. Bernoulli, har
adskillige mærkelige Egenskaber, der findes
udledte i de fleste Lærebøger i rationel Mekanik.
Den er saaledes
Løsning paa den
isoperimentriske
Opgave: Find
den af alle plane
Buer med
samme Længde, der
ved Drejning om
en Akse i dens
Plan beskriver
det mindste
Areal, idet
Buens
Endepunkter har en given
Beliggenhed i
Forhold til
Aksen. Dette er
en Følge af
den
barycentriske Regel (s. d.), efter hvilken det
beskrevne Areal er = Buens Længde
multipliceret med Omkredsen af den Cirkel, som dens
Tyngdepunkt beskriver; stilles Aksen (X)
nemlig vandret, falder iflg. Ligevægtslæren
Tyngdepunktet saa nær ved Aksen som muligt, naar
Buen antager K.’s Form. K.’s Ligning i et
retvinklet Koordinatsystem med vandret X-Akse
og Y-Aksen gaaende gennem det laveste Punkt
(B) er y = h/2 (_e x/h _+e — x/h)> hvor e er
Grundtallet for de naturlige Logaritmer og h en
Konstant.
Chr. C.

Kædelinie.

Kæden, se Kædeordenen.

Kædenitning ell. Siksaknitning
kaldes det Arrangement af Nitterne i en
Forbindelse med to ell. fl. Nitterækker bag hinanden,
hvor Nitterne i den ene Række sidder ud for
Mellemrummene i den foreg. og efterflg. Række.
Modsætningen hertil er Parallelnitning,
hvor Nitterne i alle Rækker sættes lige ud for
hinanden.
A. O-d.

Kædeordenen ell., som dens fulde Navn
lyder, Kæden de tre vise af Østerland
er et hemmeligt, væsentlig filantropisk Selskab,
hvis Oprindelse gaar langt tilbage i Tiden, og
som i fl. Henseender minder om de gl. »Gilder«.
K. formodes at være ophørt i Slutn. af 17. Aarh.,
men fornyedes, iflg. den af Selskabet udgivne
Matrikel, 27. Novbr 1774. I Beg. af 19. Aarh.
paatog K. sig to Opgaver, som siden har hørt
til dens faste Virksomhed: Omsorgen for Blinde
og for Fattiges Bespisning om Vinteren. K. er

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>