Salmonsens konversationsleksikon / Anden Udgave / Bind XXII: Spekulation—Søøre / 810 (1915-1930) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Svingninger

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

μ² = 4 m k1, saa at vi lige netop faar en
aperiodisk Bevægelse. Man kalder dette
Bevægelsestilfælde for det aperiodiske Grænsetilfælde.

3) Tvungne harmoniske
Svingninger. Vi har ovenfor tænkt os
Svingningerne bestemt af det svingende Systems egne
Egenskaber: Massen m, Kraftkoefficienten k1 og
Gnidningskoefficienten μ. Man kalder saadanne
Svingninger for Egensvingninger. Det
forekommer imidlertid hyppigt, at en udefra
kommende periodisk Kraft med en anden
Svingningstid paavirker Legemet og tvinger
det til at svinge med denne. Man kalder
saadanne Svingninger for tvungne
Svingninger; de fremkommer for Eksempel ved
Paavirkning af en ensartet Række (Lyd-, Vand-,
elektriske) Bølger af en bestemt Bølgelængde
ell. i Teknikken ved Paavirkning, hidrørende
fra Vekselstrømme ell. roterende Maskiner. Vi
tænker os Størrelsen af den ydre Kraft paa
Massen m givet ved Formlen k0 sin 2 t/T0, d. v. s.
at Kraften er harmonisk svingende med
Perioden T0 og Maksimalværdi k0. Til at begynde
med vil Massen m faa en Bevægelse, der er
sammensat af dens Egensvingninger med
Svingningstiden T1 og dens tvungne Svingninger med
Svingningstiden T0, men de førstnævnte er
dæmpede, medens de sidste stadig holdes
vedlige af den ydre Kraft. Naar der er gaaet
nogen Tid efter Bevægelsens Begyndelse, vil
derfor Egensvingningerne være døet hen, og den
tvungne Svingning med Perioden T0 vil være
alene tilbage. Amplituden i denne Bevægelse
vil være proportional med k0, men vil desuden
afhænge stærkt af Størrelsen af
Svingningstiden T0 i Forhold til Størrelsen af
Egensvingningstiden T1. Tænker man sig den ydre Krafts
Amplitude k0 holdt konstant, medens dens
Svingningstid T0 efterhaanden antager alle
mulige Værdier, vil de tilsvarende Amplituder af
Massedelens tvungne Svingning variere efter de
i Fig. 3 viste Kurver, der svarer til svingende
Systemer med samme Egenfrekvens, men
forskellig Dæmpning. Man ser, at Amplituden er
størst for en vis Værdi af T0. Denne Værdi
vil paa det nærmeste falde sammen med
Værdien for Egenperioden T1. Man siger, at der
for denne Værdi er Resonans mellem den
paatvunghe Periode og Egenperioden. En Kurve,
der angiver Amplitudens Afhængighed ell.
almindeligvis den kinetiske Energis Afhængighed
af den paatvungne Svingningstid T0, kalder
man en Resonanskurve. Dens Forløb er
bestemt ved Størrelsen af Dæmpningen. Er
denne stor, bliver Kurven lav og flad (Kurve II
og III paa Fig. 3), er den derimod lille, bliver
Resonanskurvens maksimale Del høj og smal
(Kurve I). Da Dæmpningen bestemmer
Formen af Resonanskurven, kan man omvendt af
en iagttagen Kurve beregne Dæmpningens
Størrelse. Af Resonansens Egenskab ved ringe
Dæmpning at give meget store Udslag for en
enkelt Frekvens, gør man Brug i forsk. fysiske
Instrumenter, som f. Eks. Frekvensmaalere ved
afstemte Fjedre og Vibrationsgalvanometret.
Ved andre Apparater, som f. Eks. Telefonen,
ønsker man netop, at der skal være saa lille
Forskel som muligt i Membranens Udsving for
de forsk. Toner, da det ellers vilde forvrænge
Talen, i dette Tilfælde skal man derfor have
en flad Resonanskurve, altsaa stærk
Dæmpning.

Virker samtidig flere Kræfter med hver sin
Periode, faas Massedelens Bevægelse ved en
simpel Sammensætning af de Bevægelser, som
hver af disse Kræfter for sig vilde fremkalde.
Kræfternes Virkninger vil altsaa være
uafhængige af hverandre. Er Massedelens Bevægelse
kun svagt dæmpet, vil en Kraft, der er i
Resonans med dens Egensvingning, frembringe
store Udsving, medens den svingende Masse
vil være relativ ufølsom over for
Paavirkninger af andre Perioder. Ganske analoge Forhold
gælder for elektriske Svingningskredse, hvor
Resonansfænomenet ved ringe Dæmpning gør
det muligt at afstemme en Modtagerkreds,
saaledes at den af de mange Paavirkninger, den
samtidig er udsat for, udskiller den enkelte,
hvis Periode falder sammen med dens
Egenperiode. (Se nærmere Radiotelegrafi).

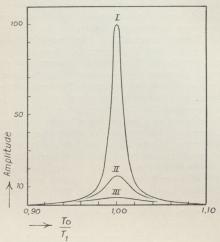Fig. 3.

4) Ikke-harmoniske Svingninger.
Saadanne vil opstaa, naar Massedelen er
paavirket af en Kraft, der ikke er proportional
med første Potens af Afstanden x fra
Ligevægtsstillingen, altsaa ikke kan skrives som
k1 . x, men har Led af højere Grad, som f.
Eks. k1 x + k2 x² + k₃ x³. Har den
svingende Bevægelse en meget lille Amplitude, vil
Leddene af højere Grader være forsvindende,
og vi faar da med Tilnærmelse en harmonisk
Sinussvingning med Egenfrekvensen n0. Er
Amplituderne derimod saa store, at de andre
Led bliver af Betydning, kan Bevægelsen ikke
længere beskrives ved et enkelt Sinusled, men
bestaar af en uendelig Række af saadanne Led
med Frekvenser, der er hele Multipla af
Grundfrekvensen n0, de saakaldte Oversvingninger
ell. (i Lydlæren) Overtoner, hvis Amplituder
er Funktioner af Udslagets Størrelse. Et
Eksempel paa en ikke-harmonisk (anharmonisk)
Svingning er Pendulets ved større Udsving; i
det hele taget vil de fleste svingende mekaniske

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>