
Full resolution (TIFF) - On this page / på denna sida - Svingninger

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
samlede Energi konstant. Naar Legemet
passerer Ligevægtsstillingen, er dets potentielle
Energi Nul, medens dets Hastighed og dermed
dets kinetiske Energi er størst (=1/2 m 4π2a2/T2). Er
Legemet kommet ud i det største Udsving a,
er Hastigheden og den kinetiske Energi Nul,
Energien er her helt omsat til potentiel Energi
(= 1/2 k1 a2). En svingende Bevægelse er
derfor karakteriseret ved en skiftevis Omdannelse
af kinetisk Energi til potentiel Energi og
omvendt.
Hvad der her er sagt om en enkelt svingende
Massedel kan i det væsentlige overdrages paa
andre mere sammensatte Systemer, der har en
enkelt Egensvingningstid, f. Eks. mange fysiske
Instrumenter som Galvanometre, Magnetnaale,
hvor der findes Drejningssvingninger om en
Akse. I Formlen for Svingningstiden skal man
da ved m forstaa det svingende Systems
Inertimoment om Svingningsaksen og ved k1
Drejningsmomentet for Fjerningsvinklen 1.
Endvidere kan Formlerne for Svingningstiden
og Energierne anvendes paa elektriske
Svingningskredse, bestaaende af en Selvinduktion og
en Kapacitet, naar man ved m forstaar
Selvinduktionskoefficienteh, ved k1 den reciproke
Værdi af Kapaciteten, og ved a den maximale
Ladning af Kapaciteten. Til den kinetiske
Energi svarer her den elektrokinetiske Energi, til
den potentielle den elektrostatiske.
2) Dæmpede harmoniske
Svingninger. Den beskrevne harmoniske
Svingningsbevægelse vil fortsætte sig i ubegrænset
Tid. I Virkeligheden vil der ved ethvert
svingende System være en vis Bevægelsesmodstand,
der vil bevirke, at Svingningerne efterhaanden
vil dø hen, med mindre der stadig udefra
tilføres Energi. Forudsætter vi nu, at det
sidstnævnte ikke er Tilfældet, vil Svingningerne
efterhaanden aftage, og man kalder da
Bevægelsen for dæmpede Svingninger.
Bevægelsesmodstanden kan hidrøre fra almindelig
Gnidningsmodstand — ved Pendulet f. Eks.
Gnidningen i Lejet og Gnidningen ved Bevægelsen
gennem Luften, hvorved Svingningsenergien
begge Steder omsættes til Varme — men den
kan ved hurtige Svingninger ogsaa hidrøre fra,
at den svingende Energi udsendes som Lyd til
Omgivelserne. Skyldes Bevægelsesmodstanden
Vædske ell. Luftgnidning, vil den ved smaa
Hastigheder være proportional med og modsat
rettet Legemets Hastighed v og vil derfor
matematisk kunne udtrykkes ved — μv, hvor μ
er en Konstant. Ogsaa Bevægelsesmodstanden
ved Lydudsendelse vil kunne bringes paa denne
Form. I saa Tilfælde faar man en dæmpet
harmonisk S., hvor Udsvinget x kan vises at
følge Formlen x — a e—μt/2m sin (2πt/T1 + q).
Bevægelsen illustreres ved Fig. 2. Den forløbne Tid er
afsat hen ad en vandret Linie, og til ethvert
Tidspunkt finder man Udslagets Størrelse som
Højden af Kurven paa det betragtede Sted.
Er Kurven over Tidslinien, betyder det, at
Udslaget er til højre, er den under den, at
Udslaget er til venstre for Ligevægtsstillingen.
Kurve I forestiller en harmonisk Bevægelse,
hvor Amplituderne holder sig uforandrede.
Kurve II en dæmpet harmonisk S. Danner man
Forholdet An/An+1 mellem to Udsving, der følger
efter hinanden med et Mellemrum af
Svingningstiden T1, vil det vise sig at være konstant
ɔ: uafhængig af Udsvingenes absolutte Størrelse.
Gaar altsaa Udsvinget efter n Svingninger ned
til Halvdelen af sin opr. Værdi, vil det efter
2n Svingninger være formindsket til
Fjerdedelen, efter 3n til Ottendedelen o. s. v. Dette
kan ogsaa udtrykkes saaledes, at Udsvingene
har konstant Logaritmedifferens. Ved
Svingningernes logaritmiske Dekrement δ
forstaas den naturlige Logaritme af Forholdet
An/An+1. (Ved svag Dæmpning vil δ med
Tilnærmelse være lig den relative Formindskelse
An—An+1/An af paa hinanden følgende Udsving).
Udtrykt ved de ovenfor indførte Størrelser er
δ = μT1/2m, og Udslaget kan ved Hjælp af δ
skrives paa Formen x = a e —δt/T1 sin (2πt/T1
φ).
For Svingningstiden T1 ved dæmpede
harmoniske Svingninger har man Udtrykket T1 =
2π kvadrarod(m/k1) · kvadratrod(1+δ2/4π2). Svingningstiden er altsaa
ligesom ved de udæmpede Svingninger
uafhængig af Udsvingenes Størrelse, men er for samme
m og k1 større end ved udæmpede
Svingninger. Dog vil Forøgelsen af Svingningstiden
være ringe, naar da Svingningerne ikke er meget
stærkt dæmpede. Bliver Bevægelsesmodstanden
meget stor, saaledes at μ2 ≧ 4 m k1, faar vi
overhovedet ikke Svingninger, men Legemet
vil, naar det fjernes fra Ligevægtsstillingen,
nærme sig den uden nogen Sinde at overskride
den. Man kalder en saadan Bevægelse
aperiodisk (Kurve III). Ved mange
Instrumenter til elektriske Maalinger ønsker man at give
de drejende ell. svingende Dele en Dæmpning,
for at Aflæsningen ikke skal tage for lang Tid.
Det gunstigste er da en Dæmpning, der gør
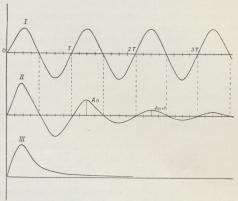 |
| Fig. 2. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>