
Full resolution (TIFF) - On this page / på denna sida - Triangulation

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Trækket ved dets Udstramning og Temperaturen ved
Jordoverfladen bestemmes) regne med en
Middelfejl, der, selv under gunstige Terrainforhold
og bortset fra Fejlen i Bestemmelsen af
Baandets Længde, næppe kan anslaas til en mindre
Værdi end omtrent 10 cm.
For at faa Kontrol til Sikring mod grove Fejl
og for tillige at opnaa Mulighed for gennem en
Udjævning af de forekommende uundgaaelige
Smaafejl at forøge Resultatets Nøjagtighed maa
man sørge for at kunne maale et tilstrækkeligt
Antal Vinkler ud over det til Trekantnettets
Bestemmelse absolut nødvendige, og har
Nettet en meget stor Udstrækning, maa man
tillige maale to eller flere Grundlinier.
Fejludjævningen udføres efter »mindste Kvadraters
Metode« (s. d.), ofte dog med Undtagelse af
Trekantnet af laveste Orden. Af den maalte
Længde og de udjævnede Vinkelværdier beregnes
Længden af de øvrige Trekantsider og dernæst
Koordinaterne til samtlige Hovedpunkter, efter
at man — ved selvstændige, større T. ad
astronomisk Vej — har bestemt Beliggenheden af et
af 1. Ordens Punkterne og maalt den Vinkel,
som en fra dette Punkt udgaaende Trekantside
danner med Nordretningen (Meridianen). Ved
selvstændige mindre T., hvor der kan ses bort
fra Jordkrumningen, beregnes retvinklede
plane Koordinater, medens man ved større T. for
de overordnede Hovedpunkters
Vedkommende ved Beregningerne maa tage Hensyn til
Jordens sfæroidiske Form (se Landmaaling
og Gradmaaling).
Ved Triangulationer, der kræves knyttede til
givne Hovedpunkter af højere Orden,
fastlægges det underordnede Nets Punkter enkeltvis
(Punktindordning), eventuelt nogle faa Punkter
ad Gangen (Netindordning), ved de Sigter,
hvorved de staar i Forbindelse med de
nærmest omliggende overordnede Punkter og
tidligere bestemte Punkter af samme Orden. —
Til de ved Punktindordninger anvendte
Bestemmelsesmaader hører de saakaldte
Skæringer, der gaar ud paa ved Vinkelmaaling
at bestemme et Punkt, P, i Forhold til givne
Punkter, A, B, C, . . ., paa en af følgende
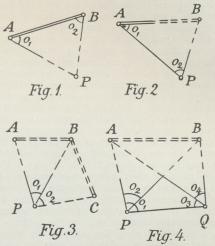
Maader: 1) ved Fremskæring ved i A og B
(Fig. 1) at sigte til P og et givet Punkt og
maale Vinklerne (o1 og o2) mellem Sigternes
Retninger; 2) ved Sideskæring ved i A
(Fig. 2) at sigte til P og et givet Punkt og i P
at sigte til A og B og maale Vinklerne (o1 og
o2) mellem Sigternes Retninger; 3) ved
Tilbageskæring (Pothenot’s Problem)
ved i P at sigte til A, B og C (Fig. 3) og
maale Vinklerne (o1 og o2) mellem Sigternes
Retninger. Ved en særlig Form af
Tilbageskæring, der kan kaldes gensidig
Tilbageskæring, men som sædvanlig benævnes
Hansen’s Problem, løses den Opgave at
bestemme to Punkter, P og Q (Fig. 4) i
Forhold til to givne Punkter, A og B, ved i
P og Q at maale de Vinkler (o1, o2, o3 og o4),
hvorunder Punkternes Forbindelseslinier ses.
— Da de under 1), 2) og 3) anførte Antal givne
Punkter er absolut nødvendige til de
paagældende Stedbestemmelsers Udførelse, maa man
for at faa Prøve (og eventuelt Udjævning af
Fejl) bestemme Retningen af et Sigte mellem
P og endnu et givet Punkt, eller man
tilvejebringer flere saadanne Overbestemmelser. —
Punktbestemmelsen ved Tilbageskæring giver
et større Koordinatberegningsarbejde end
Frem- og Sideskæring, og ved dens grafiske
Anvendelse, hvor P findes som Skæringspunkt
mellem to over Linierne AB og BC (Fig. 3) som
Korder tegnede Cirkelbuer, der rummer
henholdsvis Vinkel o1 og o2, giver den en
forholdsvis ringe Nøjagtighed. Derimod knytter der sig
til Tilbageskæringen den Fordel, at man kun
behøver at maale Vinkler i det Punkt, som
skal bestemmes, saa at de givne Punkter kan
være utilgængelige, saasom Taarnspir og
Dampskorstene, hvad der navnlig gør Metoden
anvendelig til Punktbestemmelser paa Søen (med
Vinkelmaaling ved Sekstant o. l.), ligesom den
i den nyeste Tid har faaet en særlig Anvendelse
ved Stedbestemmelser, der knytter sig til
fotogrammetriske Opmaalinger fra Luftfartøjer (se
Luftfotografering). Da Luftstationerne,
hvorfra de fotografiske Terrainbilleder
optages, imidlertid fordres bestemte baade ved
deres vandrette Projektioner og ved deres Højde
i Forhold til de givne Hovedpunkter, maa der
altsaa ved disse Stedbestemmelser arbejdes
med Rumkoordinater, og hvad der navnlig gør
Opgaven sammensat, er, at der til hver enkelt
Luftstations Stedbestemmelse paa Grundlag af
de givne Hovedpunkters Rumkoordinater og
det fra Luftfartøjet optagne Fotografi maa
udledes Udtryk til Bestemmelse af det
fotografiske Apparats Orientering i det Øjeblik, da
Optagelsen af det fotografiske Billede fandt
Sted.
Triangulationsmetoden synes at være
grundlagt af den belgiske Læge og Matematiker
Rainer Gemma-Frisius, der i sit i
1533 udgivne Skrift, Libellus de locorum
describendorum ratione, angiver Forskrifter til
Punktbestemmelser ved et Net af Trekanter bestemte
ved Fremskæring. Men det var først den
nederlandske Matematiker Willebrord
Snellius, der gav Metoden dens fulde
Udformning ved den af ham i 1614—15 udførte
 |
<< prev. page << föreg. sida << >> nästa sida >> next page >>