
Full resolution (JPEG) - On this page / på denna sida - I. Matematik, av Nils Evermark - Praktisk geometri - Linjer och vinklar
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Linjer och vinklar
Ex. Förvandla 22,655° till grader, minuter och sekunder.
0,655° = —, x = 60 • 0,655 = 39,30 = 39,3’
60
0,3’ = 1-; y = 60 • 0,3 = 18"
60
Svar: 22,655° = 22°39’18"
Ex. Förvandla 35°42’52" till decimaldelar av grader
52’ 42 87°
52" = — = 0,87’; 42,87’ = —-= 0,7145°
60 60
Svar: 35°42’52" = 35,7145°
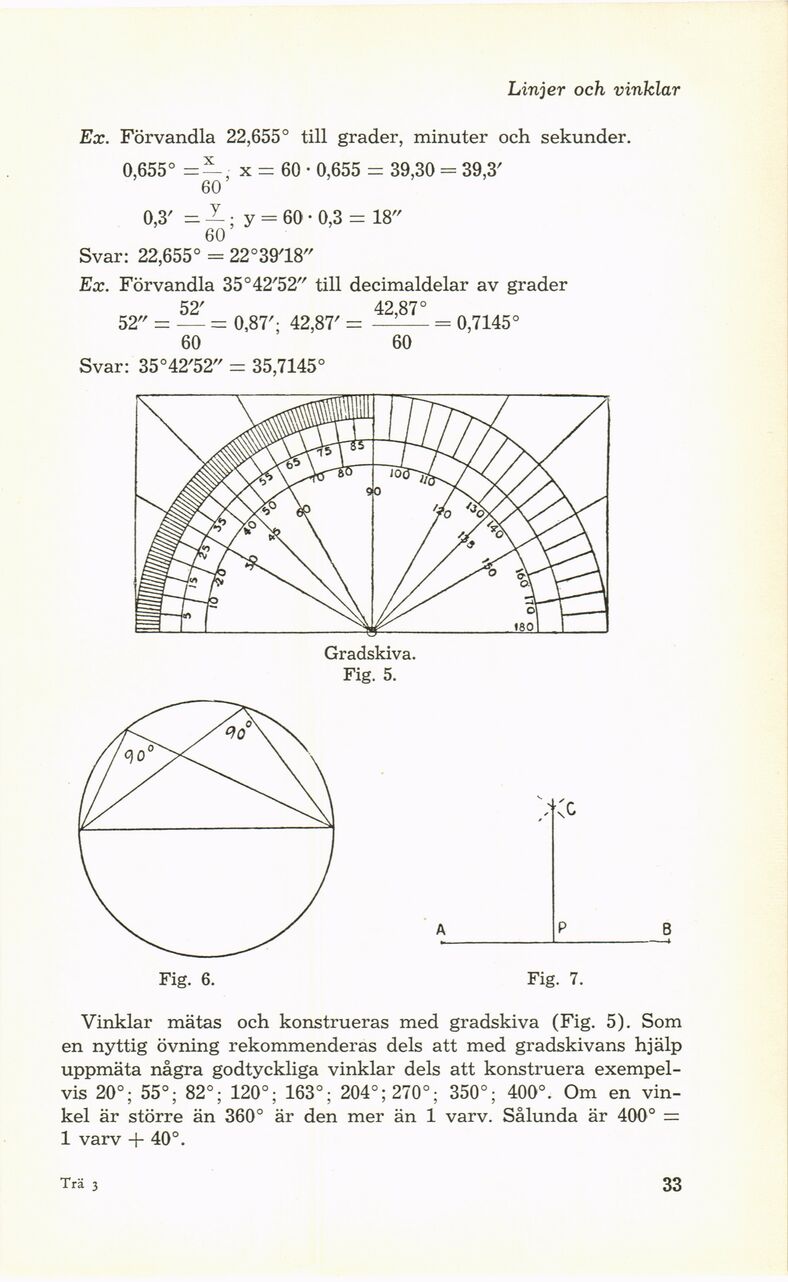
Fig. 6. Fig. 7.
Vinklar mätas och konstrueras med gradskiva (Fig. 5). Som
en nyttig övning rekommenderas dels att med gradskivans hjälp
uppmäta några godtyckliga vinklar dels att konstruera
exempelvis 20°; 55°; 82°; 120°; 163°; 204°; 270°; 350°; 400°. Om en
vinkel är större än 360° är den mer än 1 varv. Sålunda är 400° =
1 varv + 40°.
Trä 3
33
Gradskiva.
Fig. 5.
<< prev. page << föreg. sida << >> nästa sida >> next page >>