
Full resolution (TIFF) - On this page / på denna sida - Häfte 3. Mars 1933 - Carl Heuman: Mekanisk beräkning av elektriska luftledningar
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
4 MARS 1933
ELEKTROTEKNIK
35
tionen" för vågräta spänn. Om man för ett visst
"begynnelsetillstånd" känner värdena på y och g, låt
vara y’, fi’, ävensom temperaturen f, kan man av
tillståndsekvationen bestämma det mot y och s
svarande värdet A’, vilket då gäller vid temperaturen
t’. Det för en godtycklig temperatur t gällande
värdet A erhålles därefter av ekv. (8). Varje
belastnings- och temperaturtillstånd svarar då mot
bestämda värden e, h och tillståndsekvationen ger
sedan det häremot svarande värdet y.
Uppgiften att beräkna inflytandet av variationer i
belastningen och temperaturen är därmed principiellt
löst. För den praktiska användningen behöver man
en enkel metod att finna det värde på A, resp. y. som
enligt tillståndsekvationen svarar mot givna värden
på de båda andra koefficienterna. Denna ekvation
har närmare bestämt formen
där då F^(y) och F2(y) äro vissa funktioner enbart av
y. Den kan därför representeras genom ett
nomogram, där y, s och 2 representeras av punkter på var
sin skala på sådant sätt, att samhöriga värden av
dessa storheter motsvaras av tre punkter i rät linje.
Få grund av ekvationens form bliva därvid skalorna
för s och h uppburna av två räta linjer. Dessa kunna
speciellt väljas parallella, då de motsvarande
skalorna bli reguljära. Däremot blir y-skalan uppburen
av en kroklinje, bestämd av de i (10) ingående
funktionerna F^(y) OCh F2(y).
Det är nu detta nomogram, som är framställt i
diagrammet ^guS1, om vars utseende fig. 2 ger en
föreställning. De båda rätliniga skalorna äro
graderade för 104e och 1041 resp., medan den krokliniga
skalan på ena sidan uppbär en gradering för y, på den
andra - som ovan nämnts - för 102/?. Ett enkelt
exempel torde tillräckligt belysa diagrammets
användning.
Ex. En koppartråd med genomskärningsytan
A - 25 mm2, egna vikten q = 0,225 kg/m,
elasticitets-modylen E = 12 000 kg/mm2 och
Litvidgningskoeffi-cienten a = 17 . 10~6 upplägges vid +20°C på
spännvidden a - 200 m med en nedhängning 5 = 8
in. Huru stora bliva nedhängningen och påkänningen
vid - 40°C?
Man får 104£ = Wqa : E A = 1,5 och 102£ =
= 102& : a =z 4. Genom de härav bestämda
punkterna på de motsvarande skalorna i 3)£T<S lägger
man en rät linje (prickad i reproduktionen i fig. 2).
Där denna linje skär ^-skalan, kan man avläsa
104^ = 37,8. Detta värde gäller då vid temperaturen
t’ - + 20CC, så att T = 37,8 . 10~4. För det värde
l, som gäller vid -40°C, erhålles av ekv. (8) 1041=:
= 37,8 -17 . 10~~2 - 60 = 27,6. Genom de punkter,
som motsvara värdena 104£ - 1,5 och lO4^, = 27,6,
lägger man nu en ny rät linje (ävenledes prickad i
fig. 2) och avläser i dess skärningspunkt med den
krokliniga skalan y - 3,5)6 och 102/? =. 3,52, varav
beräknas l O2 0 : y = 0,99. Vid -40° blir då
nedhängningen = 10~2- 3,52 . 200 z= 7,04 m. Då vidare x = ’qa:
: A =z 1,8 kg/mm2, blir vid samma temperatur
hori-sontalpåkänningen OH = 3,56 ^ = 6,41 kg/mm2 och
i Diagram för tillståndsekvationen.
O At A, A2
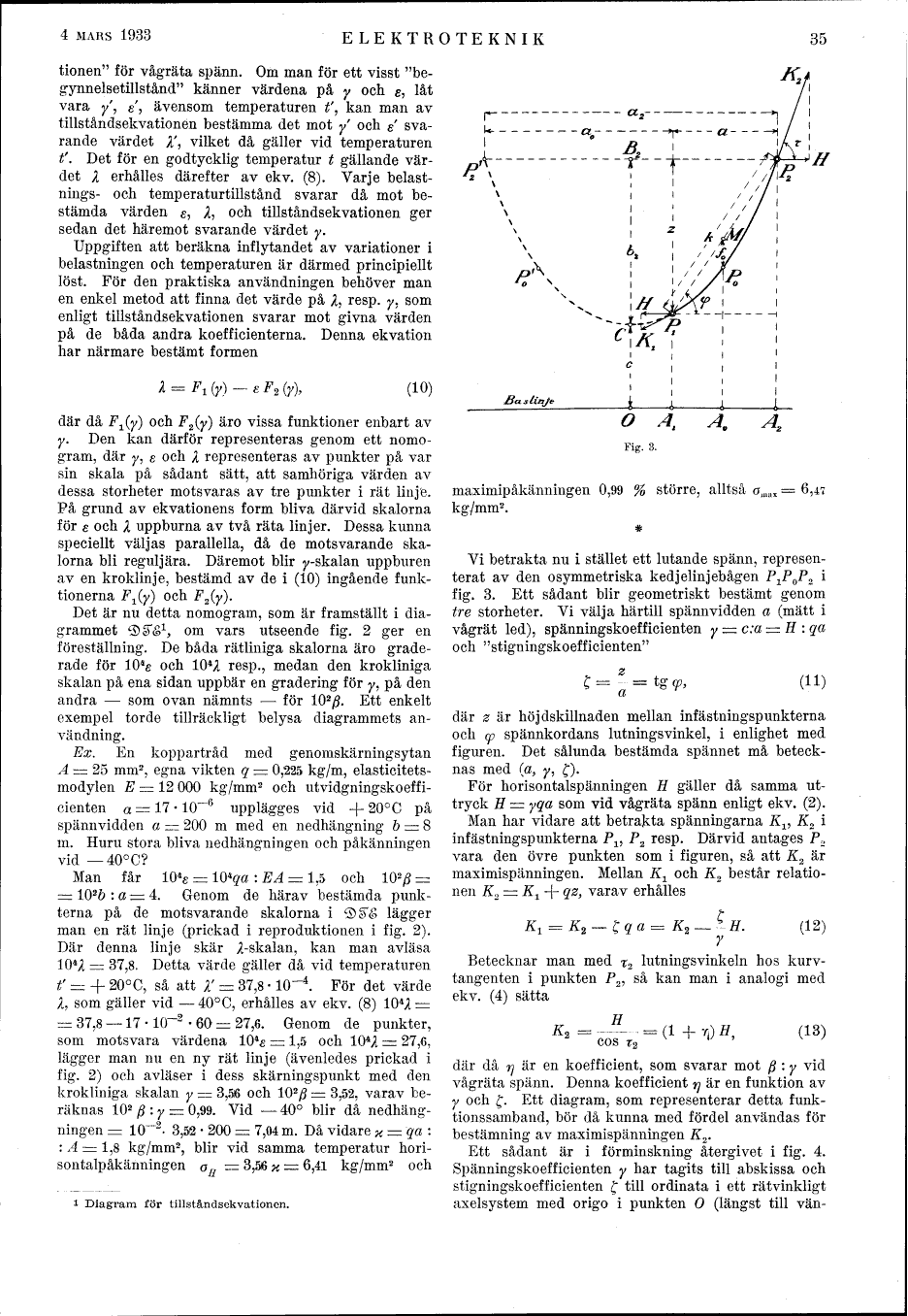
Fig. 3.
maximipåkänningen 0,99 % större, alltså amax = 6,47
kg/mm2.
Vi betrakta nu i stället ett lutande spänn,
representerat av den osymmetriska kedjelinjebågen PIP()P2 i
fig. 3. Ett sådant blir geometriskt bestämt genom
tre storheter. Vi välja härtill spännvidden a (mätt i
vågrät led), spänningskoefficienten y =. c:a - E : ga
och "stigningskoefficienten"
<p,
(ii)
där z är höjdskillnaden mellan infästningspunkterna
och y spännkordans lutningsvinkel, i enlighet med
figuren. Det sålunda bestämda spännet må
betecknas med (a, y, £).
För horisontalspänningen H gäller då samma
uttryck E - yqa som vid vågräta spänn enligt ekv. (2).
Man har vidare att betrakta spänningarna K1? K2 i
infästningspunkterna P±, P2 resp. Därvid antages P2
vara den övre punkten som i figuren, så att K2 är
maximispänningen. Mellan K^ och K2 består
relationen K2 =z KI + qz, varav erhålles
C q a = K2 - *-
(12)
Betecknar man med r2 lutningsvinkeln hos
kurv-tangenten i punkten P2, så kan man i analogi med
ekv. (4) sätta
- = (1+1) H,
(13)
där då r\ är en koefficient, som svarar mot ^ : y vid
vågräta spänn. Denna koefficient r\ är en funktion av
y och f. Ett diagram, som representerar detta
funktionssamband, bör då kunna med fördel användas för
bestämning av maximispänningen K2.
Ett sådant är i förminskning återgivet i fig. 4.
Spänningskoefficienten y har tagits till abskissa och
stigningskoefficienten f till ordinata i ett rätvinkligt
axelsystem med origo i punkten O (längst till vän-
<< prev. page << föreg. sida << >> nästa sida >> next page >>