Teknisk Tidskrift / 1933. Mekanik / 87 (1871-1962) Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (TIFF) - On this page / på denna sida - Häfte 8. Augusti 1933 - Joel Björklund: En analys av prov med stållinor

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

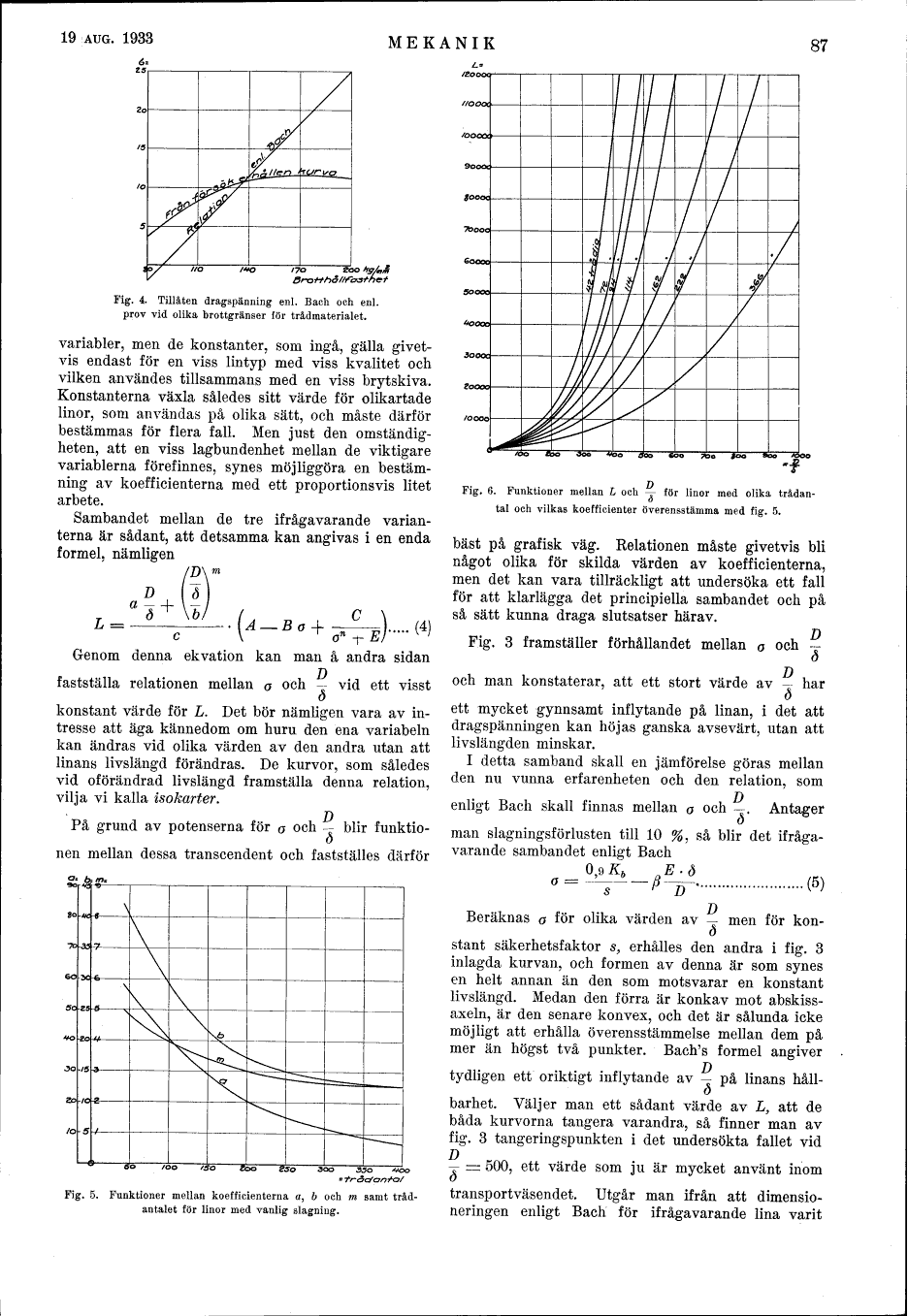
Fig. 4. Tillåten dragspänning enl. Bach och enl. prov vid olika brottgränser för trådmaterialet.

variabler, men de konstanter, som ingå, gälla
givetvis endast för en viss lintyp med viss kvalitet och
vilken användes tillsammans med en viss brytskiva.
Konstanterna växla således sitt värde för olikartade
linor, som användas på olika sätt, och måste därför
bestämmas för flera fall. Men just den omständigheten,
att en viss lagbundenhet mellan de viktigare
variablerna förefinnes, synes möjliggöra en bestämning
av koefficienterna med ett proportionsvis litet arbete.

Sambandet mellan de tre ifrågavarande varianterna
är sådant, att detsamma kan angivas i en enda
formel, nämligen

	a D / [delta] + D / [delta] / bm		C
L =	––––––––––––––––––	. ( A – B o +	––––––	) . . . (4)
	c		on + E

Genom denna ekvation kan man å andra sidan
fastställa relationen mellan o och D / [delta] vid ett visst
konstant värde för L. Det bör nämligen vara av
intresse att äga kännedom om huru den ena variabeln
kan ändras vid olika värden av den andra utan att
linans livslängd förändras. De kurvor, som således
vid oförändrad livslängd framställa denna relation,
vilja vi kalla isokarter.

På grund av potenserna för o och D / [delta] blir funktionen
mellan dessa transcendent och fastställes därför

Fig. 5. Funktioner mellan koefficientern a, b och m samt trådantalet för linor med vanlig slagning.

Fig. 6. Funktioner mellan L och D / [delta] för linor med olika trådantal och vilkas koefficienter överensstämma med fig. 5.

bäst på grafisk väg. Relationen måste givetvis bli
något olika för skilda värden av koefficienterna,
men det kan vara tillräckligt att undersöka ett fall
för att klarlägga det principiella sambandet och på
så sätt kunna draga slutsatser härav.

Fig. 3 framställer förhållandet mellan o och D / [delta]
och man konstaterar, att ett stort värde av D / [delta] har
ett mycket gynnsamt inflytande på linan, i det att
dragspänningen kan höjas ganska avsevärt, utan att
livslängden minskar.

I detta samband skall en jämförelse göras mellan
den nu vunna erfarenheten och den relation, som
enligt Bach skall finnas mellan o och D / [delta] . Antager
man slagningsförlusten till 10 %, så blir det
ifrågavarande sambandet enligt Bach

	0,9 Kb		E . [delta]
o =	––––––	– [beta]	––––––	. . . . (5)
	s		D

Beräknas o för olika värden av D / [delta] men för
konstant säkerhetsfaktor s, erhålles den andra i fig. 3
inlagda kurvan, och formen av denna är som synes
en helt annan än den som motsvarar en konstant
livslängd. Medan den förra är konkav mot
abskissaxeln, är den senare konvex, och det är sålunda icke
möjligt att erhålla överensstämmelse mellan dem på
mer än högst två punkter. Bach’s formel angiver
tydligen ett oriktigt inflytande av D / [delta] på linans håll-
barhet. Väljer man ett sådant värde av L, att de
båda kurvorna tangera varandra, så finner man av
fig. 3 tangeringspunkten i det undersökta fallet vid
D / [delta] 500, ett värde som ju är mycket använt inom
transportväsendet. Utgår man ifrån att dimensioneringen
enligt Bach för ifrågavarande lina varit

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>