
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Mekanik
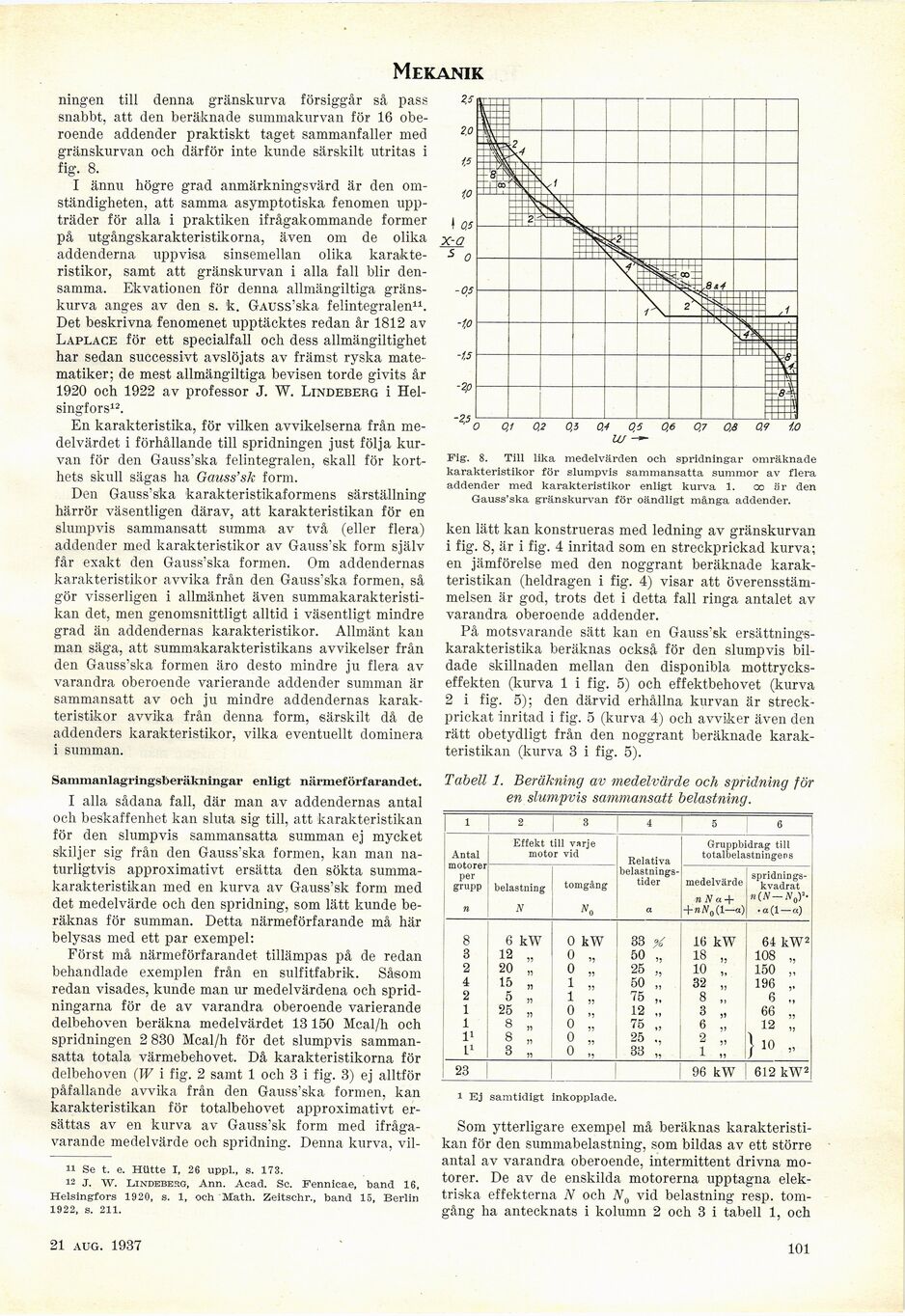
ningen till denna gränskurva försiggår så pass
snabbt, att den beräknade summakurvan för 16
oberoende addender praktiskt taget sammanfaller med
gränskurvan och därför inte kunde särskilt utritas i
fig. 8.
I ännu högre grad anmärkningsvärd är den
omständigheten, att samma asymptotiska fenomen
uppträder för alla i praktiken ifrågakommande former
på utgångskarakteristikorna, även om de olika
addenderna uppvisa sinsemellan olika
karakte-ristikor, samt att gränskurvan i alla fall blir
densamma. Ekvationen för denna allmängiltiga
gränskurva anges av den s. k. GAUSs’ska felintegralen11.
Det beskrivna fenomenet upptäcktes redan år 1812 av
Laplace för ett specialfall och dess allmängiltighet
har sedan successivt avslöjats av främst ryska
matematiker; de mest allmängiltiga bevisen torde givits år
1920 och 1922 av professor J. W. Lindeberg i
Helsingfors12.
En karakteristika, för vilken avvikelserna från
medelvärdet i förhållande till spridningen just följa
kurvan för den Gauss’ska felintegralen, skall för
korthets skull sägas ha Gauss’sk form.
Den Gauss’ska karakteristikaformens särställning
härrör väsentligen därav, att karakteristikan för en
slumpvis sammansatt summa av två (eller flera)
addender med karakteristikor av Gauss’sk form själv
får exakt den Gauss’ska formen. Om addendernas
karakteristikor avvika från den Gauss’ska formen, så
gör visserligen i allmänhet även
summakarakteristi-kan det, men genomsnittligt alltid i väsentligt mindre
grad än addendernas karakteristikor. Allmänt kan
man säga, att summakarakteristikans avvikelser från
den Gauss’ska formen äro desto mindre ju flera av
varandra oberoende varierande addender summan är
sammansatt av och ju mindre addendernas
karakteristikor avvika från denna form, särskilt då de
addenders karakteristikor, vilka eventuellt dominera
i summan.
Sammanlagringsberäkningar enligt närmeförfarandet.
I alla sådana fall, där man av addendernas antal
och beskaffenhet kan sluta sig till, att karakteristikan
för den slumpvis sammansatta summan ej mycket
skiljer sig från den Gauss’ska formen, kan man
naturligtvis approximativt ersätta den sökta
summa-karakteristikan med en kurva av Gauss’sk form med
det medelvärde och den spridning, som lätt kunde
beräknas för summan. Detta närmeförfarande må här
belysas med ett par exempel:
Först må närmeförfarandet tillämpas på de redan
behandlade exemplen från en sulfitfabrik. Såsom
redan visades, kunde man ur medelvärdena och
spridningarna för de av varandra oberoende varierande
delbehoven beräkna medelvärdet 13150 Mcal/h och
spridningen 2 830 Mcal/h för det slumpvis
sammansatta totala värmebehovet. Då karakteristikorna för
delbehoven (W i fig. 2 samt 1 och 3 i fig. 3) ej alltför
påfallande avvika från den Gauss’ska formen, kan
karakteristikan för totalbehovet approximativt
ersättas av en kurva av Gauss’sk form med
ifrågavarande medelvärde och spridning. Denna kurva, vil-
II Se t. e. Hütte I, 26 uppl., s. 173.
12 J. W. Lindebesg, Ann. Acad. Se. Fennieae, band 16,
Helsingfors 1920, s. 1, oeh Math. Zeitschr., band 15, Berlin
1922, s. 211.
Fig. 8. Till lika medelvärden och spridningar omräknade
karakteristikor för slumpvis sammansatta summor av flera
addender med karakteristikor enligt kurva 1. co är den
Gauss’ska gränskurvan för oändligt många addender.
ken lätt kan konstrueras med ledning av gränskurvan
1 fig. 8, är i fig. 4 inritad som en streckprickad kurva;
en jämförelse med den noggrant beräknade
karakteristikan (heldragen i fig. 4) visar att
överensstämmelsen är god, trots det i detta fall ringa antalet av
varandra oberoende addender.
På motsvarande sätt kan en Gauss’sk
ersättnings-karakteristika beräknas också för den slumpvis
bildade skillnaden mellan den disponibla
mottrycks-effekten (kurva 1 i fig. 5) och effektbehovet (kurva
2 i fig. 5); den därvid erhållna kurvan är
streck-prickat inritad i fig. 5 (kurva 4) och avviker även den
rätt obetydligt från den noggrant beräknade
karakteristikan (kurva 3 i fig. 5).
Tabell 1. Beräkning av medelvärde och spridning för
en slumpvis sammansatt belastning.
1 2 3 4 5 6
Antal Effekt till varje motor vid Relativa Gruppbidrag till totalbelastningens
per grupp n belastning N tomgång »0 [-belastningstider-] {+belastnings- tider+} a medelvärde n N a + + nN0( l-«) spridniDgs- kvadrat n(N-N0Y• .a(l-a)
8 6 kW 0 kW 33 ^ 16 kW 64 kW2
3 12 „ 0 „ 50 „ 18 „ 108 „
2 20 „ 0 „ 25 „ 10 „ 150 „
4 15 „ 1 „ 50 „ 32 „ 196 „
2 5 „ 1 „ 75 „ 8 „ 6 „
1 25 „ 0 „ 12 „ 3 „ 66 „
I 8 „ 0 „ 75 „ 6 „ 12 „
II 8 „ 0 „ 25 ., 2 „ ) 10
t1 3 „ 0 „ 33 „ 1 „ f 10 "
23___!_^_96 kW ’ 612 kW2
i Ej samtidigt inkopplade.
Som ytterligare exempel må beräknas
karakteristikan för den summabelastning, som bildas av ett större
antal av varandra oberoende, intermittent drivna
motorer. De av de enskilda motorerna upptagna
elektriska effekterna N och N0 vid belastning resp.
tomgång ha antecknats i kolumn 2 och 3 i tabell 1, och
21 aug. 1937
101
<< prev. page << föreg. sida << >> nästa sida >> next page >>