
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
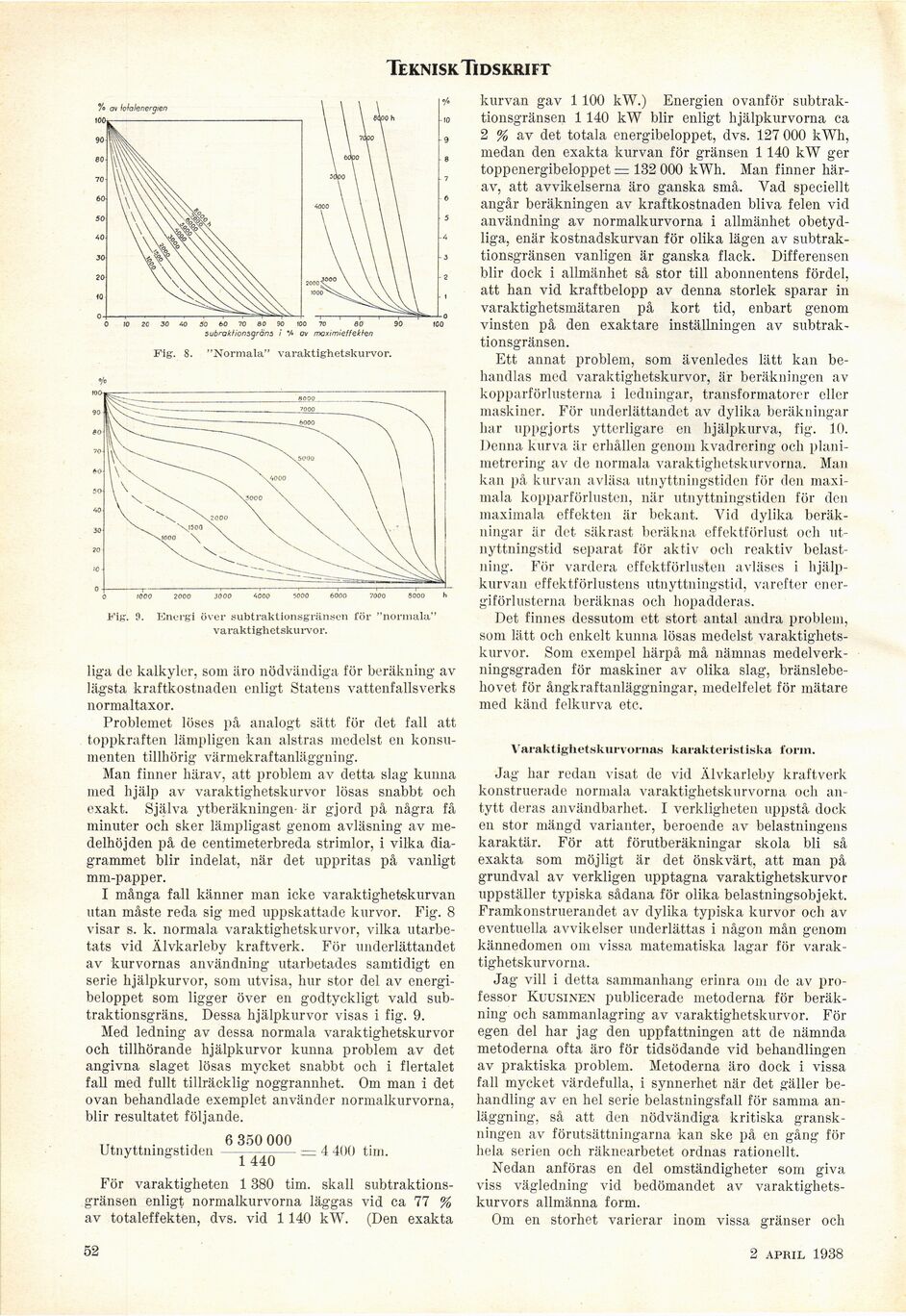
Fig. 8. "Normala" varaktighetskurvor.
Fig. 9. Energi över subtraktionsgränsen för "normala"
varaktighetskurvor.
liga de kalkyler, som äro nödvändiga för beräkning av
lägsta kraftkostnaden enligt Statens vattenfallsverks
normaltaxor.
Problemet löses på analogt sätt för det fall att
toppkraften lämpligen kan alstras medelst en
konsumenten tillhörig värmekraftanläggning.
Man finner härav, att problem av detta slag kunna
med hjälp av varaktighetskurvor lösas snabbt och
exakt. Själva ytberäkningen- är gjord på några få
minuter och sker lämpligast genom avläsning av
medelhöjden på de centimeterbreda strimlor, i vilka
diagrammet blir indelat, när det uppritas på vanligt
mm-papper.
I många fall känner man icke varaktighetekurvan
utan måste reda sig med uppskattade kurvor. Fig. 8
visar s. k. normala varaktighetskurvor, vilka
utarbetats vid Älvkarleby kraftverk. För underlättandet
av kurvornas användning’ utarbetades samtidigt en
serie hjälpkurvor, som utvisa, hur stor del av
energibeloppet som ligger över en godtyckligt väld
subtraktionsgräns. Dessa hjälpkurvor visas i fig. 9.
Med ledning av dessa normala varaktighetskurvor
och tillhörande hjälpkurvor kunna problem av det
angivna slaget lösas mycket snabbt och i flertalet
fall med fullt tillräcklig noggrannhet. Om man i det
ovan behandlade exemplet använder normalkurvorna,
blir resultatet följande.
6 350 000
Utnyttningstiden - — 4 400 tim.
J ö 1 440
För varaktigheten 1380 tim. skall
subtraktionsgränsen enligt normalkurvorna läggas vid ca 77 %
av totaleffekten, dvs. vid 1140 kW. (Den exakta
kurvan gav 1100 kW.) Energien ovanför
subtraktionsgränsen 1140 kW blir enligt hjälpkurvorna ca
2 % av det totala energibeloppet, dvs. 127 000 kWh,
medan den exakta kurvan för gränsen 1140 kW ger
toppenergibeloppet = 132 000 kWh. Man finner
härav, att avvikelserna äro ganska små. Vad speciellt
angår beräkningen av kraftkostnaden bliva felen vid
användning av normalkurvorna i allmänhet
obetydliga, enär kostnadskurvan för olika lägen av
subtraktionsgränsen vanligen är ganska flack. Differensen
blir dock i allmänhet så stor till abonnentens fördel,
att han vid kraftbelopp av denna storlek sparar in
varaktighetsmätaren på kort tid, enbart genom
vinsten på den exaktare inställningen av
subtraktionsgränsen.
Ett annat problem, som ävenledes lätt kan
behandlas med varaktighetskurvor, är beräkningen av
kopparförlusterna i ledningar, transformatorer eller
maskiner. För underlättandet av dylika beräkningar
har uppgjorts ytterligare en hjälpkurva, fig. 10.
Denna kurva är erhållen genom kvadrering och
plani-metrering av de normala varaktighetskurvorna. Man
kan på kurvan avläsa utnyttningstiden för den
maximala kopparförlusten, när utnyttningstiden för den
maximala effekten är bekant. Viel dylika
beräkningar är det säkrast beräkna effektförlust och
ut-nyttningstid separat för aktiv ocli reaktiv
belastning. För vardera effektförlusten avläses i
hjälp-kurvan effektförlustens utnyttningstid, varefter
energiförlusterna beräknas och hopadderas.
Det finnes dessutom ett stort antal ändra problem,
som lätt och enkelt kunna lösas medelst
varaktighetskurvor. Som exempel härpå må nämnas
medelverkningsgraden för maskiner av olika slag,
bränslebe-liovet för ångkraftanläggningar, medelfelet för mätare
med känd felkurva etc.
Varaktighetskurvoriias karakteristiska form.
Jag har redan visat de vid Älvkarleby kraftverk
konstruerade normala varaktighetskurvorna och
antytt deras användbarhet. I verkligheten uppstå dock
en stor mängd varianter, beroende av belastningens
karaktär. För att förutberäkningar skola bli så
exakta som möjligt är det önskvärt, att man på
grundval av verkligen upptagna varaktighetskurvor
uppställer typiska sådana för olika belastningsobjekt.
Framkonstruerandet av dylika typiska kurvor och av
eventuella avvikelser underlättas i någon mån genom
kännedomen om vissa matematiska lagar för
varaktighetskurvorna.
Jag vill i detta sammanhang erinra om de av
professor Kuusinen publicerade metoderna för
beräkning och sammanlagring av varaktighetskurvor. För
egen del har jag den uppfattningen att de nämnda
metoderna ofta äro för tidsödande vid behandlingen
av praktiska problem. Metoderna äro dock i vissa
fall mycket värdefulla, i synnerhet när det gäller
behandling av en hel serie belastningsfall för samma
anläggning, så att den nödvändiga kritiska
granskningen av förutsättningarna kan ske på en gång för
hela serien ocli räknearbetet ordnas rationellt.
Nedan anföras en del omständigheter som giva
viss vägledning vid bedömandet av
varaktighetskurvors allmänna form.
Om en storhet varierar inom vissa gränser och
52
2 april 1938
<< prev. page << föreg. sida << >> nästa sida >> next page >>