
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
TekniskTidskrift
(po = <p2 — <P l",
s» .
^=2 V
953 = <Pt-CpRi
+
9-1 = -1-
— arc tg — 1 — tg a + a;
A, =<p0[R?°- Ä2J - <p3R* +
\
i’
(5)
(6)
R0 = grundcirkelns radie = Rd eos a,
Rd — delningscirkelns radie,
Rt — toppcirkelns radie,
R = Rt — s-
Den sökta av frasen utskurna kuggluckans area är
således:
A,
ns(2R-\-s)
(7)
z — kugghjulets antal tänder.
Ekv. (6) måste tyvärr beräknas med logaritmer,
emedan termerna äro varandra inbördes ganska lika
t.ill sin numeriska valör.
Sätter man
13
* = c • -g m\ (8)
där c— en konstant < 1,
får man lätt, att As och A, äro proportionella med m-.
Man behöver således endast beräkna (6) för en
modul exempelvis m = 1 och för olika c-värden, varefter
man erhåller önskade värden för andra moduler
genom att multiplicera med m-,
I fig. 7 har jag beräknat två st. kurvor enligt (1)
och (6) och sålunda för z — 00 och z — 39 samt
m = 1.
För exempelvis 20° ingreppsvinkel får man, om
man insätter ekv. (8) i ekv. 1 (sifferräkningen utförd
på sticka).
^| = 1,72 C (C+0,91). (9)
Ekv. [(6) och (7)] kunna på samma sätt göras
dimensionslösa genom insättning av:
Rt = m[t +
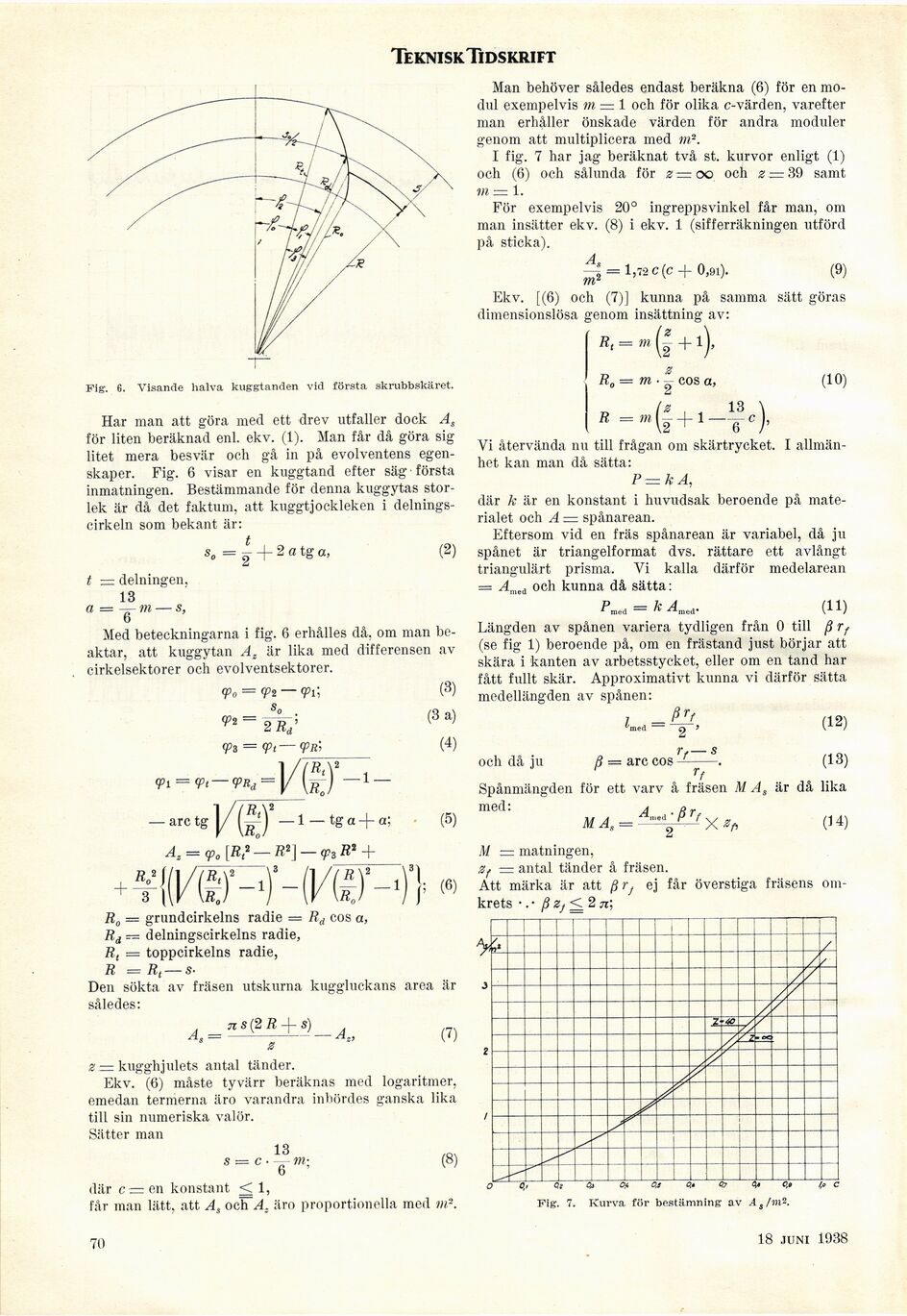
Fig. 6. Visande halva kuggtanden vid första skrubbskäret.
Har man att göra med ett drev utfaller dock As
för liten beräknad enl. ekv. (1). Man får då göra sig
litet mera besvär och gå in på evolventens
egenskaper. Fig. 6 visar en kuggtand efter säg första
inmatningen. Bestämmande för denna kuggytas
storlek är då det faktum, att kuggtjockleken i
delnings-cirkeln som bekant är:
So=| + 2atga, (2)
t — delningen,
13
a = — s,
o
Med beteckningarna i fig. 6 erhålles då, om man
beaktar, att kuggytan Az är lika med differensen av
cirkelsektorer och evolventsektorer.
(3)
(3 a)
(4)
t
— m ■ c
= m( f-
R0— m ■ — eos a,
dt
1
(10)
13
6
4
Vi återvända nu till frågan om skärtrycket. I
allmänhet kan man då sätta:
P ~k A,
där k är en konstant i huvudsak beroende på
materialet och A — spånarean.
Eftersom vid en fräs spånarean är variabel, då ju
spånet är triangelformat dvs. rättare ett avlångt
triangulärt prisma. Vi kalla därför medelarean
= Amed och kunna då sätta:
■^med = & -^med-
(11)
Längden av spånen variera tydligen från 0 till ß rf
(se fig 1) beroende på, om en frästand just börjar att
skära i kanten av arbetsstycket, eller om en tand har
fått fullt skär. Approximativt kunna vi därför sätta
medellängden av spånen:
l
Ved - g ’
och då ju ß = arc eos ——
(12)
Spånmängden för ett varv å fräsen M As är
raed: A.^-ßrf,
MA, =
M = matningen,
gf — antal tänder å fräsen.
Att märka är att ß r}
krets •. • ß z/< 2 n;
X Zf.
(13)
lika
(14)
ej får överstiga fräsens om-
O,t Qi Qi O/i Oj 0,è Oj c)# 0,9
Fig. 7. Kurva för bestämning av A . /«i2
c
70
18 juni 1938
<< prev. page << föreg. sida << >> nästa sida >> next page >>