
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
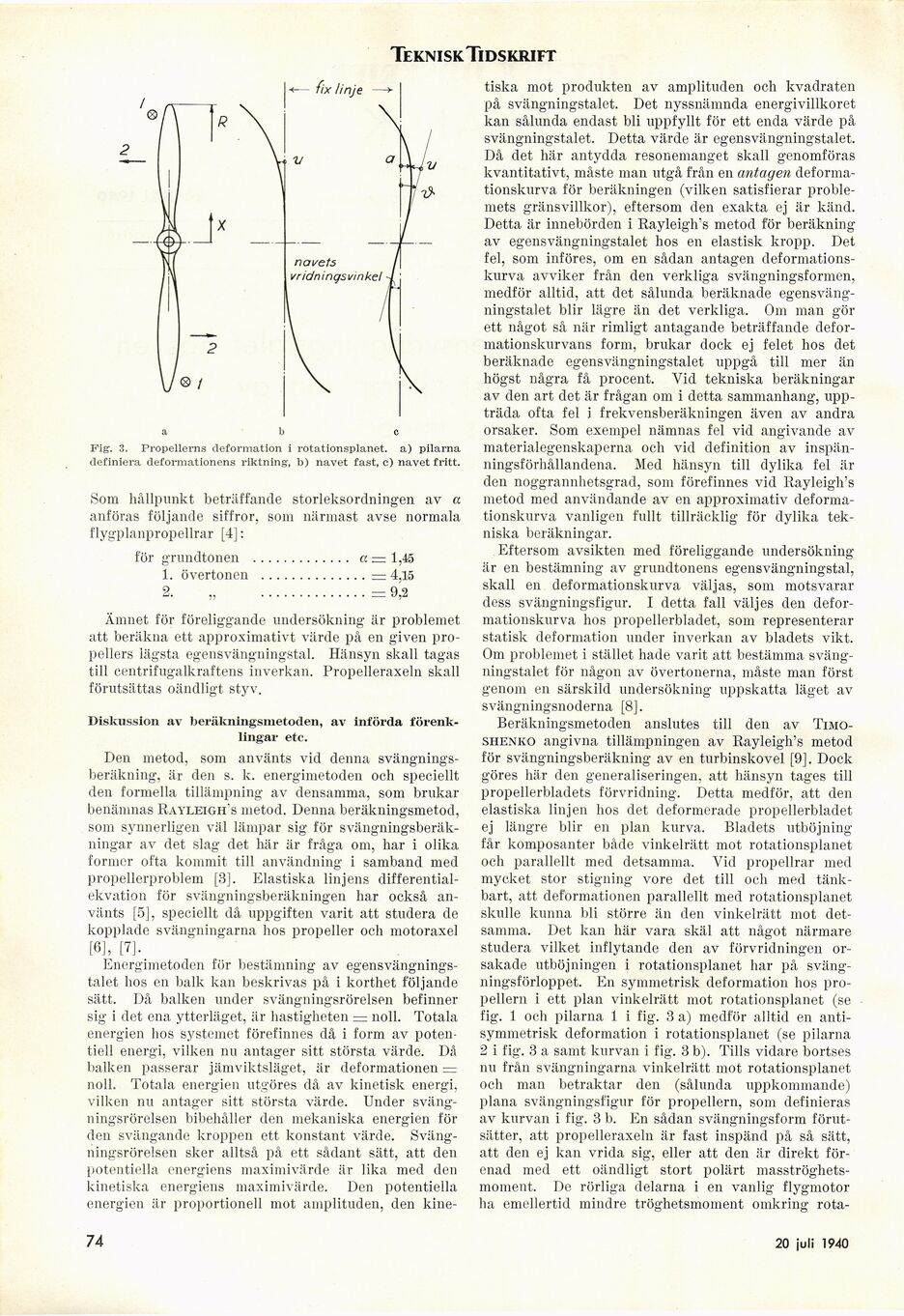
navets
vridn ings vinkel
Fig. 3. Propellerns deformation i rotationsplanet, a) pilarna
definiera deformationens riktning, b) navet fast, c) navet fritt.
Som hållpunkt beträffande storleksordningen av a
anföras följande siffror, som närmast avse normala
flygplanpropellrar [4]:
för grundtonen ............. a = 1,45
1. övertonen ..............= 4,15
2. „ ..............=9,2
Ämnet för föreliggande undersökning är problemet
att beräkna ett approximativt värde på en given
propellers lägsta egensvängningstal. Hänsyn skall tagas
till centrifugalkraftens inverkan. Propelleraxeln skall
förutsättas oändligt styv.
Diskussion av beräkningsmetoden, av införda
förenklingar etc.
Den metod, som använts vid denna
svängningsberäkning, är den s. k. energimetoden och speciellt
den formella tillämpning av densamma, som brukar
benämnas Rayleighs metod. Denna beräkningsmetod,
som synnerligen väl lämpar sig för
svängningsberäkningar av det slag det här är fråga om, har i olika
former ofta kommit till användning i samband med
propellerproblem [3]. Elastiska linjens
differentialekvation för svängningsberäkningen har också
använts [5], speciellt då uppgiften varit att studera de
kopplade svängningarna hos propeller och motoraxel
[6], [7].
Energimetoden för bestämning av
egensvängningstalet hos en balk kan beskrivas på i korthet följande
sätt. Då balken under svängningsrörelsen befinner
sig i det ena ytterläget, är hastigheten = noll. Totala
energien hos systemet förefinnes då i form av
potentiell energi, vilken nu antager sitt största värde. Då
balken passerar jämviktsläget, är deformationen =
noll. Totala energien utgöres då av kinetisk energi,
vilken nu antager sitt största värde. Under
svängningsrörelsen bibehåller den mekaniska energien för
den svängande kroppen ett konstant värde.
Svängningsrörelsen sker alltså på ett sådant sätt, att den
potentiella energiens maximivärde är lika med den
kinetiska energiens maximivärde. Den potentiella
energien är proportionell mot amplituden, den kine-
tiska mot produkten av amplituden och kvadraten
på svängningstalet. Det nyssnämnda energivillkoret
kan sålunda endast bli uppfyllt för ett enda värde på
svängningstalet. Detta värde är egensvängningstalet.
Då det här antydda resonemanget skall genomföras
kvantitativt, måste man utgå från en antagen
deformationskurva för beräkningen (vilken satisfierar
problemets gräns villkor), eftersom den exakta ej är känd.
Detta är innebörden i Rayleigh’s metod för beräkning
av egensvängningstalet hos en elastisk kropp. Det
fel, som införes, om en sådan antagen
deformations-kurva avviker från den verkliga svängningsformen,
medför alltid, att det sålunda beräknade
egensvängningstalet blir lägre än det verkliga. Om man gör
ett något så när rimligt antagande beträffande
deformationskurvans form, brukar dock ej felet hos det
beräknade egensvängningstalet uppgå till mer än
högst några få procent. Vid tekniska beräkningar
av den art det är frågan om i detta sammanhang,
uppträda ofta fel i frekvensberäkningen även av andra
orsaker. Som exempel nämnas fel vid angivande av
materialegenskaperna och vid definition av
inspän-ningsförhållandena. Med hänsyn till dylika fel är
den noggrannhetsgrad, som förefinnes vid Rayleigh’s
metod med användande av en approximativ
deformationskurva vanligen fullt tillräcklig för dylika
tekniska beräkningar.
Eftersom avsikten med föreliggande undersökning
är en bestämning av grundtonens egensvängningstal,
skall en deformationskurva väljas, som motsvarar
dess svängningsfigur. I detta fall väljes den
deformationskurva hos propellerbladet, som representerar
statisk deformation under inverkan av bladets vikt.
Om problemet i stället hade varit att bestämma
svängningstalet för någon av övertonerna, måste man först
genom en särskild undersökning uppskatta läget av
svängningsnoderna [8].
Beräkningsmetoden anslutes till den av
Timo-shenko angivna tillämpningen av Rayleigh’s metod
för svängningsberäkning av en turbinskovel [9], Dock
göres här den generaliseringen, att hänsyn tages till
propellerbladets förvridning. Detta medför, att den
elastiska linjen hos det deformerade propellerbladet
ej längre blir en plan kurva. Bladets utböjning
får komposanter både vinkelrätt mot rotationsplanet
och parallellt med detsamma. Vid propellrar med
mycket stor stigning vore det till och med
tänkbart, att deformationen parallellt med rotationsplanet
skulle kunna bli större än den vinkelrätt mot
detsamma. Det kan här vara skäl att något närmare
studera vilket inflytande den av förvridningen
orsakade utböjningen i rotationsplanet har på
svängningsförloppet. En symmetrisk deformation lios
propellern i ett plan vinkelrätt mot rotationsplanet (se
fig. 1 och pilarna 1 i fig. 3 a) medför alltid en
anti-symmetrisk deformation i rotationsplanet (se pilarna
2 i fig. 3 a samt kurvan i fig. 3 b). Tills vidare bortses
nu från svängningarna vinkelrätt mot rotationsplanet
och man betraktar den (sålunda uppkommande)
plana svängningsfigur för propellern, som definieras
av kurvan i fig. 3 b. En sådan svängningsform
förutsätter, att propelleraxeln är fast inspänd på så sätt,
att den ej kan vrida sig, eller att den är direkt
förenad med ett oändligt stort polärt
masströghets-moment. De rörliga delarna i en vanlig flygmotor
ha emellertid mindre tröghetsmoment omkring1 rota-
74
20 juli 1940
<< prev. page << föreg. sida << >> nästa sida >> next page >>